已知在平面直角坐标系
中的一个椭圆，它的中心在原点，左焦点为
,右顶点为
,设点
.
（1）求该椭圆的标准方程；
（2）若
是椭圆上的动点，求线段
中点
的轨迹方程；
（3）过原点
的直线交椭圆于点
，求
面积的最大值。
已知椭圆
，直线
与椭圆交于A、B两点，M是线段AB的中点，连接OM并延长交椭圆于点C．直线AB与直线OM的斜率分别为k、m，且
．
（1）求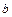
的值；
(2）若直线AB经过椭圆的右焦点F，问：对于任意给定的不等于零的实数k，是否存在a∈
，使得四边形OACB是平行四边形，请证明你的结论；
已知集合A＝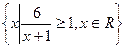
，B＝{x|x2－2x－m<0}，
(1)当m＝3时，求A∩(∁RB)；
(2)若A∩B＝{x|－1<x<4}，求实数m的值
已知椭圆E：
（
0）过点（0，
），其左焦点
与点P（1，
）的连线与圆
相切。
（1）求椭圆E的方程；
（2）设Q为椭圆E上的一个动点，试判断以
为直径的圆与圆
的位置关系，并证明
如图，P—ABCD是正四棱锥，
是正方体，其中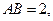
（1）求证：
；
（2）求平面PAD与平面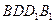
所成的锐二面角
的余弦值；
（3）求
到平面PAD的距离
在△ABC中，a、b是方程x2－2mx+2=0的两根，且2cos(A+B)=-1
(1)求角C的度数；
(2)求△ABC的面积