如图,P—ABCD是正四棱锥, 是正方体,其中
是正方体,其中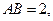

(1)求证: ;
;
(2)求平面PAD与平面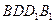 所成的锐二面角
所成的锐二面角 的余弦值;
的余弦值;
(3)求 到平面PAD的距离
到平面PAD的距离
已知命题p: 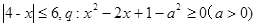 ,若非p是q的充分不必要条件,求a的取值范围。
,若非p是q的充分不必要条件,求a的取值范围。
直线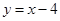 与抛物线
与抛物线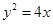 交于A、B两点,F为抛物线的焦点,求△ABF的面积。
交于A、B两点,F为抛物线的焦点,求△ABF的面积。
(满分10分)设函数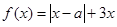 ,其中
,其中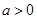 .
.
(Ⅰ)当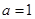 时,求不等式
时,求不等式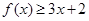 的解集;
的解集;
(Ⅱ)若不等式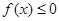 的解集为
的解集为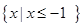 ,求
,求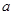 的值.
的值.
(满分12分)已知曲线C的极坐标方程 是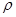 =1,以极点为原点,极轴为
=1,以极点为原点,极轴为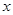 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线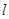 的参数方程为
的参数方程为 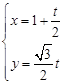 (t为参数)。
(t为参数)。
(Ⅰ)写出直线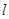 的直角坐标方程与曲线C的普通方程;
的直角坐标方程与曲线C的普通方程;
(Ⅱ)曲线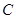 经过伸缩变换
经过伸缩变换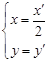 得到曲线
得到曲线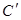 ,设曲线
,设曲线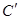 上任一点为
上任一点为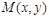 ,求
,求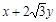 的的最小值;
的的最小值;
(满分12分)一台机器使用的时间较长,但还可以使用,它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器运转的速度而变化,下表为抽样试验的结果:
| 转速x(转/秒) |
16 |
14 |
12 |
8 |
| 每小时生产有缺点的零件数y(件) |
11 |
9 |
8 |
5 |
(Ⅰ)画出散点图;
(Ⅱ)如果y对x有线性相关关系,求回归直线方程;
(Ⅲ)若实际生产中,允许每小时的产品中有缺点的零件最多为10个,那么机器的运转速度应控制在什么范围内?
参考公式: