某校学生会有高一年级6人、高二年级5人、高三年级4人组成,
(1)选其中一人为校学生会主席,则不同的选有多少种;
(2)从3个年级中各选一个人出席一个会议,不同的选法有多少种;
(3)选不同年级的两人参加市里组织的活动,则不同的选法为多少种
设函数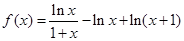 .
.
(Ⅰ)求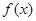 的单调区间和极值;
的单调区间和极值;
(Ⅱ)是否存在实数 ,使得关于
,使得关于 的不等式
的不等式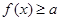 的解集为
的解集为 ?若存在,求
?若存在,求 的取值范围;若不存在,试说明理由.
的取值范围;若不存在,试说明理由.
设椭圆E: 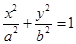 (a,b>0)过M(2,
(a,b>0)过M(2,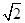 ) ,N(
) ,N(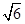 ,1)两点,O为坐标原点,
,1)两点,O为坐标原点,
(I)求椭圆E的方程;
(II)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且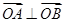 ?若存在,写出该圆的方程,并求|AB|的取值范围,若不存在说明理由
?若存在,写出该圆的方程,并求|AB|的取值范围,若不存在说明理由
如图,在底面为直角梯形的四棱锥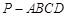 中
中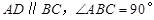 ,
, 平面
平面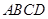 ,
,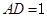 ,
, ,
, .
.
⑴求证: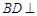
 ;
;
⑵求直线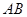 与平面
与平面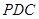 所成的角;
所成的角;
⑶设点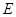 在棱
在棱 上,
上, ,若
,若 ∥平面
∥平面 ,求
,求 的值.
的值.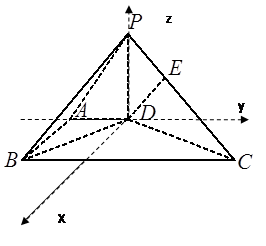
符合下列三个条件之一,某名牌大学就可录取:
①获国家高中数学联赛一等奖(保送录取,联赛一等奖从省高中数学竞赛优胜者中考试选拔);
②自主招生考试通过并且高考分数达到一本分数线(只有省高中数学竞赛优胜者才具备自主招生考试资格);
③高考分数达到该大学录取分数线(该大学录取分数线高于一本分数线).
某高中一名高二数学尖子生准备报考该大学,他计划:若获国家高中数学联赛一等奖,则保送录取;若未被保送录取,则再按条件②、条件③的顺序依次参加考试.
已知这名同学获省高中数学竞赛优胜奖的概率是0.9,通过联赛一等奖选拔考试的概率是0.5,通过自主招生考试的概率是0.8,高考分数达到一本分数线的概率是0.6,高考分数达到该大学录取分数线的概率是0.3.
(I)求这名同学参加考试次数 的分布列及数学期望;
的分布列及数学期望;
(II)求这名同学被该大学录取的概率.
对于给定数列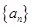 ,如果存在实常数
,如果存在实常数 ,使得
,使得 对于任意
对于任意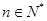 都成立,我们称数列
都成立,我们称数列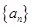 是 “
是 “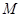 类数列”.
类数列”.
(Ⅰ)已知数列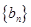 是 “
是 “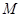 类数列”且
类数列”且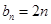 ,求它对应的实常数
,求它对应的实常数 的值;
的值;
(Ⅱ)若数列 满足
满足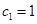 ,
, ,求数列
,求数列 的通项公式.并判断
的通项公式.并判断 是否为“
是否为“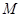 类数列”,说明理由.
类数列”,说明理由.