已知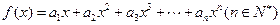 ,满足
,满足 ,
,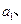


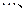
 构成数列
构成数列 。
。
(1)求数列 的通项公式; (2)证明:
的通项公式; (2)证明: 。
。
已知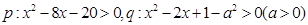 .若
.若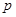 是
是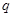 的充分而不必要条件,求正实数
的充分而不必要条件,求正实数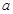 的取值范围。
的取值范围。
已知函数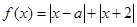 (a为常数,且a∈R).
(a为常数,且a∈R).
(1)若函数f (x)的最小值为2,求a的值;
(2)当a=2时,解不等式f (x)≤6.
在极坐标系中,已知两点O(0,0),B(2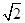 ,
,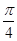 ).
).
(1)求以OB为直径的圆C的极坐标方程,然后化成直角方程;
(2)以极点O为坐标原点,极轴为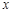 轴的正半轴建立平面直角坐标系,直线l的参数方程为
轴的正半轴建立平面直角坐标系,直线l的参数方程为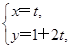 (t为参数).若直线l与圆C相交于M,N两点,圆C的圆心为C,求DMNC的面积.
(t为参数).若直线l与圆C相交于M,N两点,圆C的圆心为C,求DMNC的面积.
如图,已知C、F是以AB为直径的半圆 上的两点,且CF=CB,过C作CD^AF交AF的延长线与点D.
上的两点,且CF=CB,过C作CD^AF交AF的延长线与点D.
(1)证明:CD为圆O的切线;
(2)若AD=3,AB=4,求AC的长.
(本小题满分12分)
设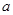 ∈R,函数
∈R,函数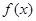 =
=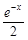 (
(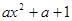 ),其中e是自然对数的底数.
),其中e是自然对数的底数.
(1)判断f (x)在R上的单调性;
(2)当– 1 <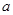 < 0时,求f (x)在[1,2]上的最小值.
< 0时,求f (x)在[1,2]上的最小值.
选做题:请考生从给出的3道题中任选一题做答,并在答题卡上把所选题目的题号用2B铅笔涂黑.注意所做题目的题号必须与所涂的题号一致,在答题卡选答区域指定位置答题.如果多做,则按所做的第一题计分.