椭圆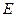 经过点
经过点 ,对称轴为坐标轴,焦点
,对称轴为坐标轴,焦点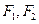 在
在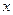 轴上,离心率
轴上,离心率 。
。
(Ⅰ)求椭圆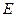 的方程;
的方程;
(Ⅱ)求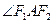 的角平分线所在直线的方程。
的角平分线所在直线的方程。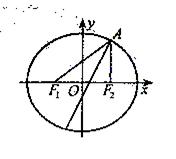
若数列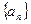 满足前n项之和
满足前n项之和 ,
,
求:(1)bn;
(2) 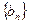 的前n项和Tn。
的前n项和Tn。
已知数列 的首项为
的首项为 =3,通项
=3,通项 与前n项和
与前n项和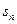 之间满足2
之间满足2 =
=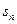 ·
·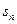
 (n≥2)。
(n≥2)。
(1)求证: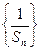 是等差数列,并求公差;
是等差数列,并求公差;
(2)求数列 的通项公式。
的通项公式。
 个正数排成如下表所示的
个正数排成如下表所示的 行
行 列:
列: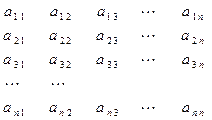
其中每一行成等差数列,每一列成等比数列,且各列的公比相等,若 ,
, ,
,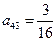 。
。
①求 ;
;
②记 ,求
,求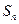 关于
关于 的表达式;
的表达式;
③对于②的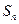 ,求证:
,求证: ;
;
④若集合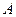 是集合
是集合 的真子集,则称由
的真子集,则称由 的判断到
的判断到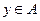 的判断为对
的判断为对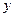 的估计的一次
的估计的一次
优化。请你优化③中的结果。
某地预计从年初开始的前 个月内,对某种商品的需求总量
个月内,对某种商品的需求总量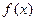 (万件)与月份
(万件)与月份 的近似关系为
的近似关系为 。
。
①写出今年第 个月的需求量
个月的需求量 (万件)与月份
(万件)与月份 的函数关系,并求出哪些个月份的需求量超过1.4万件;
的函数关系,并求出哪些个月份的需求量超过1.4万件;
②如果将该商品每月初都投放市场 万件,要保证每个月都能满足供应,则
万件,要保证每个月都能满足供应,则 至少为多少万件?
至少为多少万件?