(13分)在直角△ABC中AB=4,BC=3,AC=5,将此三角形绕AB边所在直线旋转一周得到一个圆锥
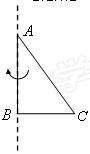
(1)求圆锥的侧面积和体积;
(2)求这个圆锥的内切球的表面积。
(本小题满分10分)已知等比数列 (I)求数列
(I)求数列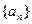 的通项公式;(II)设
的通项公式;(II)设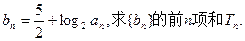
(本小题满分12分)设函数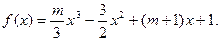
(I)若函数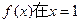 处取得极值,求此时函数
处取得极值,求此时函数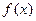 的单调区间;
的单调区间;
(II)已知不等式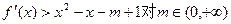 恒成立,求x的取值范围。
恒成立,求x的取值范围。
已知函数
,
,其中
.
(I)设函数
.若
在区间
上不单调,求
的取值范围;
(II)设函数
是否存在
,对任意给定的非零实数
,存在惟一的非零实数
,使得
成立?若存在,求
的值;若不存
在,请说明理由.
如图,平面
平面
,
是以
为斜边的等腰直角三角形,
分别为
,
,
的中点,
,
.
(I)设
是
的中点,证明:
平面
;
(II)证明:在
内存在一点
,使
平面
,并求点
到
,
的距离.
在1,2,3…,9,这9个自然数中,任取3个数.
(Ⅰ)求这3个数中,恰有一个是偶数的概率;
(Ⅱ)记
为这三个数中两数相邻的组数,(例如:若取出的数1、2、3,则有两组相邻的数1、2和2、3,此时
的值是2)。求随机变量
的分布列及其数学期望