(本小题满分12分)某人上楼梯,每步上一阶的概率为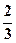 ,每步上二阶的概率为
,每步上二阶的概率为 ,设该人从台阶下的平台开始出发,到达第n阶的概率为
,设该人从台阶下的平台开始出发,到达第n阶的概率为 。
。
(Ⅰ)求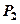 ;(Ⅱ)该人共走了5步,求
;(Ⅱ)该人共走了5步,求 该人这5步共上的阶数ξ的数学期望。
该人这5步共上的阶数ξ的数学期望。
已知函数 ,
,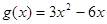 ,又函数
,又函数 在
在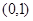 单调递减,而在
单调递减,而在 单调递增.
单调递增.
(1)求 的值;
的值;
(2)求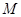 的最小值,使对
的最小值,使对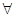
 ,有
,有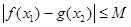 成立;
成立;
(3)是否存在正实数 ,使得
,使得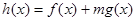 在
在 上既有最大值又有最小值?若存在,求出m的取值范围;若不存在,请说明理由.
上既有最大值又有最小值?若存在,求出m的取值范围;若不存在,请说明理由.
已知 .经计算得
.经计算得 ,
,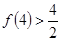 ,
, ,
,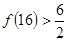 ,
, ,通过观察,我们可以得到一个一般性的结论.
,通过观察,我们可以得到一个一般性的结论.
(1)试写出这个一般性的结论;
(2)请用数学归纳法证明这个一般性的结论;
(3)对任一给定的正整数 ,试问是否存在正整数
,试问是否存在正整数 ,使得
,使得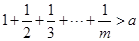 ?
?
若存在,请给出符合条件的正整数 的一个值;若不存在,请说明理由.
的一个值;若不存在,请说明理由.
阅读下面材料:
根据两角和与差的正弦公式,有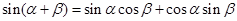 ------①
------①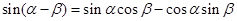 ------②
------②
由①+② 得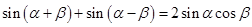 ------③
------③
令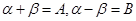 有
有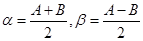
代入③得 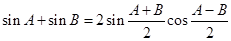 .
.
(1) 类比上述推理方法,根据两角和与差的余弦公式,证明: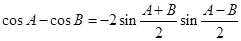 ;
;
(2)若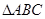 的三个内角
的三个内角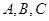 满足
满足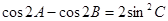 ,直接利用阅读材料及(1)中的结论试判断
,直接利用阅读材料及(1)中的结论试判断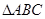 的形状.
的形状.
从5名女同学和4名男同学中选出4人参加四场不同的演讲,分别按下列要求,各有多少种不同选法?
(Ⅰ)男、女同学各2名;
(Ⅱ)男、女同学分别至少有1名;
(Ⅲ)在(Ⅱ)的前提下,男同学甲与女同学乙不能同时选出.
已知复数 在复平面内所对应的点为
在复平面内所对应的点为 .
.
(1)若复数 为纯虚数,求实数
为纯虚数,求实数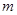 的值;
的值;
(2)若点 在第二象限,求实数
在第二象限,求实数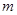 的取值范围;
的取值范围;
(3)求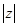 的最小值及此时实数
的最小值及此时实数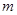 的值.
的值.