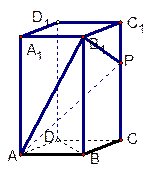
如图,在长方体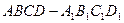 中,
中,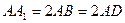 ,且
,且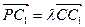
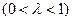 .
.
(Ⅰ)求证:对任意 ,总有
,总有 ;
;
(Ⅱ)若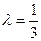 ,求二
,求二 面角
面角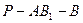 的余弦值;
的余弦值;
(Ⅲ)是否存在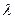 ,使得
,使得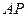 在平面
在平面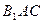 上的射影平分
上的射影平分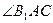 ?若存在,求出
?若存在,求出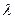 的值,若不存在,说明理由.
的值,若不存在,说明理由.
(本小题满分12分)关于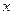 的不等式
的不等式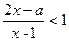 的解集为P, 不等式
的解集为P, 不等式 的解集为Q,若P
的解集为Q,若P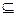 Q,求实数
Q,求实数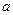 的取值范围。
的取值范围。
若定义在R上的函数 对任意的
对任意的 ,都有
,都有 成立,且当
成立,且当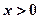 时,
时,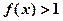 。
。
(1)求证: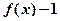 为奇函数;
为奇函数;
(2)求证: 是R上的增函数;
是R上的增函数;
(3)设集合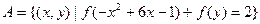 ,
, ,且
,且 , 求实数
, 求实数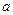 的取值范围。
的取值范围。
(本题12分)若二次函数满足 。
。
(1) 求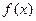 的解析式;
的解析式;
(2) 若在区间[-1,1]上不等式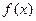 >2x+m恒成立,求实数m的取值范围。
>2x+m恒成立,求实数m的取值范围。
已知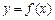 是定义在R上的函数,对于任意的
是定义在R上的函数,对于任意的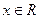 ,
, ,且当
,且当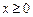 时,
时,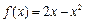 .
.
(1)求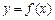 的解析式;
的解析式;
(2)画出函数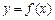 的图象,并指出
的图象,并指出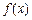 的单调区间及在每个区间上的增减性;
的单调区间及在每个区间上的增减性;
(3)若函数f(x)在区间[-1,a-2]上单调递增,试确定a的取值范围.
函数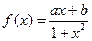 是定义在
是定义在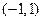 上的奇函数,且
上的奇函数,且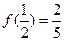 ,
,
(1)确定函数 的解析式;
的解析式;
(2)判断 在
在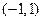 上的单调性并用定义证明.
上的单调性并用定义证明.
(3)解不等式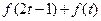 <0;
<0;