已知函数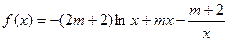
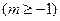 .
.
(Ⅰ)讨论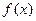 的单调性;
的单调性;
(Ⅱ)设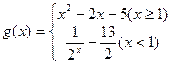 .当
.当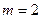 时,若对任意
时,若对任意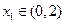 ,
,
存在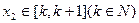 ,使
,使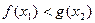 ,求实数
,求实数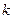 的最小值
的最小值
已知函数 (其中
(其中 )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为 ,且图象上一个最低点为
,且图象上一个最低点为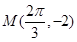 .
.
(1)求 的解析式;(2)当
的解析式;(2)当 ,求
,求 的值域.
的值域.
已知
(1)求 ;
;
(2)求向量 在向量
在向量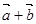 方向上的投影.
方向上的投影.
已知函数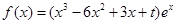 ,
,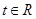 .
.
(Ⅰ)若函数 依次在
依次在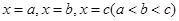 处取到极值.求
处取到极值.求 的取值范围;
的取值范围;
(Ⅱ)若存在实数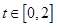 ,使对任意的
,使对任意的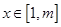 ,不等式
,不等式  恒成立.求正整数
恒成立.求正整数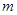 的最大值.
的最大值.
如图,边长为2的正方形ABCD,E是BC的中点,沿AE,DE将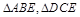 折起,使得B与C重合于O.
折起,使得B与C重合于O.
(Ⅰ)设Q为AE的中点,证明:QD AO;
AO;
(Ⅱ)求二面角O—AE—D的余弦值.
袋子中装有大小形状完全相同的m个红球和n个白球,其中m,n满足m>n≥2且m+n≤l0(m,n∈N+),若从中取出2个球,取出的2个球是同色的概率等于取出的2个球是异色的概率.
(Ⅰ) 求m,n的值;
(Ⅱ) 从袋子中任取3个球,设取到红球的个数为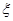 ,求
,求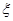 的分布列与数学期望.
的分布列与数学期望.