(本小题满分12分)已知定义在R上的单调函数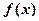 ,存在实数
,存在实数 ,使得对于任意实数
,使得对于任意实数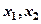 ,总有
,总有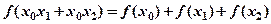 恒成立。
恒成立。
(Ⅰ)求 的值;(Ⅱ)若
的值;(Ⅱ)若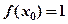 ,且对任意
,且对任意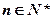 ,有
,有 ,求{an}的通项公式;
,求{an}的通项公式;
(Ⅲ)若数列{bn}满足 ,将数列{bn}的项重新组合成新数列
,将数列{bn}的项重新组合成新数列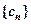 ,具体法则如下:
,具体法则如下: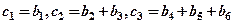 ,……,求证:
,……,求证: 。
。
已知数列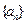 的首项
的首项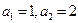 ,前
,前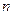 项和
项和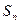 恒为正数,且当
恒为正数,且当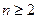 时,
时,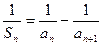 .
.
(Ⅰ)求数列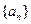 的通项公式;
的通项公式;
(Ⅱ)求证: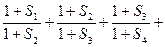
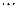
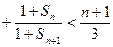 .
.
已知点 满足:
满足: (其中
(其中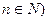 ,又知
,又知 .
.
(Ⅰ)若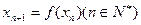 ,求
,求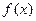 的表达式;
的表达式;
(Ⅱ)已知点 ,记
,记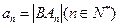 ,且
,且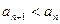 对一切
对一切 恒成立,试求
恒成立,试求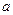 的取值范围.
的取值范围.
 如图,F是抛物线
如图,F是抛物线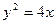 的焦点,Q为准线与
的焦点,Q为准线与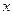 轴的交点,直线
轴的交点,直线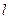 经过点Q.
经过点Q.
(Ⅰ)直线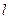 与抛物线有唯一公共点,求
与抛物线有唯一公共点,求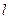 的方程;
的方程;
(Ⅱ)直线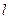 与抛物线交于A、B两点记FA、FB
与抛物线交于A、B两点记FA、FB
的斜率分别为 ,
,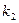 .求证:
.求证: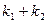 为定值.
为定值.
已知矩形ABCD中,AB=2AD=4,E为CD的中点,沿AE将三角形AED折起,使DB= ,
,
如图,O,H分别为AE、AB中点.
(Ⅰ)求证:直线OH//面BDE;
(Ⅱ)求证:面ADE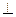 面ABCE;
面ABCE; (Ⅲ)求二面角O-DH-E的余弦值.
(Ⅲ)求二面角O-DH-E的余弦值.
某人抛掷一枚质量分布均匀的骰子,出现各数的概率都是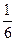 ,构造数列
,构造数列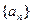 ,使
,使
 ,记
,记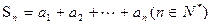 .
.
(Ⅰ)求 时的概率;
时的概率;
(Ⅱ)求前两次均为奇数且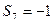 的概率.
的概率.