已知函数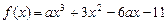 ,
,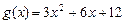 ,和直线
,和直线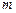 :
: .
.
又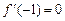 .
.
(1)求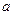 的值;
的值;
(2)是否存在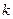 的值,使直线
的值,使直线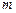 既是曲线
既是曲线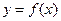 的切线,又是
的切线,又是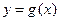 的切线;如果存在,求出k的值;如果不存在,说明理由.
的切线;如果存在,求出k的值;如果不存在,说明理由.
(3)如果对于所有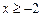 的
的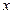 ,都有
,都有 成立,求k的取值范围.
成立,求k的取值范围.
(本小题满分12分)如图,四边形ABCD是边长为1的正方形,  ,
,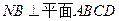 ,且MD=NB=1,E为BC的中点 (1)求异面直线NE与AM所成角的余弦值
,且MD=NB=1,E为BC的中点 (1)求异面直线NE与AM所成角的余弦值
(2)在线段AN上找点S,使得ES 平面AMN,并求线段AS的长;
平面AMN,并求线段AS的长;
(本小题满分12分)某批发市场对某商品的周销售量(单位:吨)进行统计,最近100周的统计结果如下表所示:
| 周销售量 |
2 |
3 |
4 |
| 频数 |
20 |
50 |
30 |
(1)根据上面统计结果,求周销售量分别为2吨,3吨和4吨的频率;
(2)已知每吨该商品的销售利润为2千元,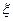 表示该种商品两周销售利润的和(单位:千元),若以上
表示该种商品两周销售利润的和(单位:千元),若以上 述频率作为概率,且各周的销售量相互独立,求
述频率作为概率,且各周的销售量相互独立,求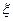 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)已知等差数列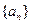 为递增数列,且
为递增数列,且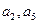 是方程
是方程 的两根,数列
的两根,数列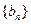 的前
的前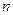 项和
项和 ;
;
(1)求数列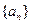 和
和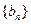 的通项公式;
的通项公式;
(2)若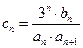 ,
,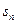 为数列
为数列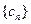 的前n项和,证明:
的前n项和,证明: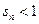
(本小题满分12分)某批发市场对某商品的周销售量(单位:吨)进行统计,最近100周的统计结果如下表所示:
| 周销售量 |
2 |
3 |
4 |
| 频数 |
20 |
50 |
30 |
(1)根据上面统计结果,求周销售量分别为2吨,3吨和4吨的频率;
(2)已知每吨该商品的销售利润为2千元,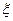 表示该种商品两周销售利润的和(单位:千元),若以上
表示该种商品两周销售利润的和(单位:千元),若以上 述频率作为概率,且各周的销售量相互独立,求
述频率作为概率,且各周的销售量相互独立,求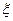 的分布列和数学期望.
的分布列和数学期望.
选修4-5:不等式证明选讲已知函数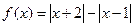 .
.
(Ⅰ)试求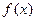 的值域;(Ⅱ)设
的值域;(Ⅱ)设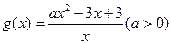 ,若对
,若对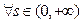 ,
, 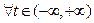 ,恒
,恒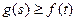 成立,试
成立,试 求实数
求实数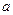 的取值范围
的取值范围