（本小题满分12分）某批发市场对某商品的周销售量（单位：吨）进行统计，最近100周的统计结果如下表所示：
| 周销售量 |
2 |
3 |
4 |
| 频数 |
20 |
50 |
30 |
(1)根据上面统计结果,求周销售量分别为2吨,3吨和4吨的频率；
(2)已知每吨该商品的销售利润为2千元,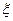
表示该种商品两周销售利润的和(单位:千元),若以上
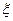述频率作为概率,且各周的销售量相互独立,求的分布列和数学期望．
已知函数
，e为自然对数的底数．
（Ⅰ）若过点A（2，f（2））的切线斜率为2，求实数a的值；
（Ⅱ）当x>0时，求证：
；
（Ⅲ）在区间（1，e）上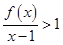
恒成立，求实数a的取值范围．
已知椭圆
的焦距为
，离心率为
．
（Ⅰ）求椭圆方程；
（Ⅱ）设过椭圆顶点B（0，b），斜率为k的直线交椭圆于另一点D，交x轴于点E，且|BD|，|BE|，|DE|成等比数列，求
的值．
等差数列
的前n项和为
，且满足
．
（Ⅰ）求数列的通项公式；
（Ⅱ）设
，数列
的前n项和为
，求证：
．
如图，在正方体
中，M，N，G分别是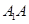
，
，AD的中点，求证：
（1）MN//平面ABCD；
（2）MN⊥平面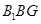
．
△ABC中内角A，B，C的对边分别为a，b，c，向量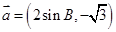
，
且
．
（1）求锐角B的大小；
（2）如果b=2，求△ABC的面积
的最大值．