(本小题满分14分)
已知等差数列 的公差大于0,且
的公差大于0,且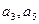 是方程
是方程 的两根,数列
的两根,数列 的前
的前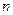 项的和为
项的和为 ,且
,且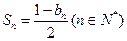 .
.
(Ⅰ) 求数列 ,
, 的通项公式;
的通项公式;
(Ⅱ) 记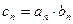 ,求证:
,求证: ;
;
(Ⅲ)求数列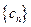 的前
的前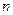 项和.
项和.
(本小题满分12分)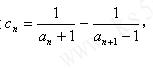
已知数列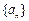 的前n项和
的前n项和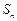 满足:
满足: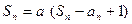 (
(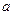 为常数,且
为常数,且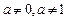 ).
).
(Ⅰ)求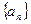 的通项公式;
的通项公式;
(Ⅱ)设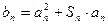 ,若数列
,若数列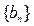 为等比数列,求
为等比数列,求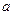 的值;
的值;
(Ⅲ)在满足条件(Ⅱ)的情形下,设,数列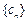 的前n项和为
的前n项和为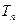 .求证:
.求证: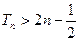 .
.
(本小题满分12分)设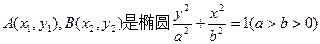 上的两点,已知向量
上的两点,已知向量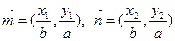 ,若
,若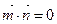 且椭圆的离心率e=,短轴长为
且椭圆的离心率e=,短轴长为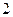 ,
,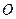 为坐标原点.
为坐标原点.
(Ⅰ)求椭圆的方程;
(Ⅱ)试问:△AOB的面积是否为定值?如果是,请给予证明;如果不是,请说明理由
(本小题满分12分)已知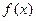 =
=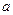
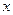 -
-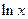 ,
,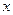 Î(0,e],其中
Î(0,e],其中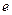 是自然常数,
是自然常数,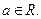
(Ⅰ)当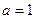 时, 求
时, 求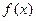 的单调区间和极值;
的单调区间和极值;
(Ⅱ)是否存在实数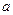 ,使
,使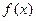 的最小值是3,若存在,求出
的最小值是3,若存在,求出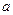 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(本小题满分12分)
“上海世博会”于2010年5月1日至10月31日在上海举行。世博会“中国馆·贵宾厅”作为接待中外贵宾的重要场所,陈列其中的艺术品是体现兼容并蓄、海纳百川的重要文化载体,为此,上海世博会事物协调局将举办“中国2010年上海世博会‘中国馆·贵宾厅’艺术品方案征集”活动。某地美术馆从馆藏的中国画、书法、油画、陶艺作品中各选一件代表作参与应征,假设代表作中中国画、书法、油画入选“中国馆·贵宾厅”
的概率均为 ,陶艺入选“中国馆·贵宾厅”的概率为
,陶艺入选“中国馆·贵宾厅”的概率为


 .
.
(Ⅰ)求该地美术馆选送的四件代表作中恰有一件作品入选“中国馆·贵宾厅”的概率;
(Ⅱ)设该地美术馆选送的四件代表作中入选“中国馆·贵宾厅”的作品件数为随机变量ξ,求ξ数学期望.
(本小题满分12分)如图,在多面体ABC-DEFG中,平面 ∥平面
∥平面 ,
, ⊥平面
⊥平面 ,
, ,
, ,
, ∥
∥ .且
.且 ,
, .
.
(Ⅰ)求证:  ∥平面
∥平面 ;
;
(Ⅱ)求二面角 的余弦值;
的余弦值;