随机观测生产某种零件的某工厂 名工人的日加工零件数(单位:件),获得数据如下:
名工人的日加工零件数(单位:件),获得数据如下: 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 ,根据上述数据得到样本的频率分布表如下:
,根据上述数据得到样本的频率分布表如下:
| 分组 |
频数 |
频率 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
 |
 |
(1)确定样本频率分布表中的值;
(2)根据上述频率分布表,画出样本频率分布直方图;
(3)根据样本频率分布直方图,求在该厂任取 人,至少有
人,至少有 人的日加工零件数落在区间
人的日加工零件数落在区间 的概率.
的概率.
已知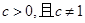 ,设
,设 :函数
:函数 在
在 上单调递减;
上单调递减; :函数
:函数 在
在 上为增函数.
上为增函数.
(1)若 为真,
为真, 为假,求实数
为假,求实数 的取值范围;
的取值范围;
(2)若“ 且
且 ”为假,“
”为假,“ 或
或 ”为真,求实数
”为真,求实数 的取值范围.
的取值范围.
在锐角 中,角
中,角 ,
, ,
, 对应的边分别是
对应的边分别是 ,
, ,
,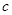 .已知
.已知 .
.
(1)求角 的大小;
的大小;
(2)若 的面积
的面积 ,
, ,求
,求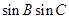 的值.
的值.
(1)平面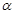 过坐标原点
过坐标原点 ,
, 是平面
是平面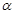 的一个法向量,求
的一个法向量,求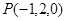 到平面
到平面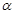 的距离;
的距离;
(2)直线 过
过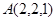 ,
, 是直线
是直线 的一个方向向量,求
的一个方向向量,求 到直线
到直线 的距离.
的距离.
已知数列 的相邻两项
的相邻两项 ,
, 是关于
是关于 方程
方程 的两根,且
的两根,且 .
.
(1)求证:数列 是等比数列;
是等比数列;
(2)求数列 的前
的前 项和
项和 ;
;
(3)设函数 ,若
,若 对任意的
对任意的 都成立,求实数
都成立,求实数 的取值范围.
的取值范围.
某投资公司计划投资A,B两种金融产品,根据市场调查与预测,A产品的利润y1与投资金额x的函数关系为y1=18- ,B产品的利润y2与投资金额x的函数关系为y2=
,B产品的利润y2与投资金额x的函数关系为y2= (注:利润与投资金额单位:万元).
(注:利润与投资金额单位:万元).
(1)该公司已有100万元资金,并全部投入A,B两种产品中,其中x万元资金投入A产品,试把A,B两种产品利润总和表示为x的函数,并写出定义域;
(2)在(1)的条件下,试问:怎样分配这100万元资金,才能使公司获得最大利润?其最大利润为多少万元?