（
本题满分13分）
如图,点A、B分别是椭圆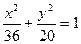
长轴的左、右端点,点F是椭圆的右焦点.点P在椭圆上,且位于x轴的上方,PA⊥PF.
(1)求点P的坐标；
(2)设M椭圆长轴AB上的一点,M到直线AP的距离等于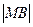
,求椭圆上的点到点M的距离d的最小值
（本小题满分12分）
已知函数
=ax3—
（1+a）x2 +3x -3（其中a∈R）
（I）若函数在x= -1时取得极值，求a；
（Ⅱ）求函数的单调区间．
（本小题满分12分）
已知函数
对任意实数x均有=kf（x+2），其中常数k为负数，且在区间[0，2]有表达式=x（x-2）
（I）求出f（-1）f（2．5）的值；
（Ⅱ）若函数在区间[ -2，2]的最大值与最小值分别为m，n，且m—n=3，求k的值。
（本小题满分12分）
设命题p：实数x满足|x-1|≤m，,其中m>0，命题q：-2<x≤10
（I）若m=2且p
q为真命题，求实数x的取值范围;
（Ⅱ）若
q是P的充分不必要条件，求实数m的取值范围．
（本小题满分10分）
化简（I）
（Ⅱ）
。
（本小题满分12分）
已知函数
= 21nx—x2+ax（a
R）
（I）当a=2时，求的图象在x=l处的切线方程；
（Ⅱ）若函数的图象与x轴有两个不同的交点A（x1，0），B（ x2，0）（0< x1< x2），
求证：
（其中
为的导函数）