已知函数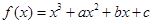 ,曲线
,曲线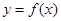 在点
在点 处的切线为
处的切线为 ,若
,若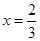 时,
时,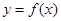 有极值.
有极值.
(1)求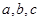 的值;
的值;
(2)求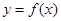 在
在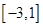 上的最大值和最小值.
上的最大值和最小值.
已知动点P与双曲线x2-y2=1的两个焦点F1,F2的距离之和为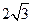 定值,
定值,
(1)求动点P的轨迹方程;
(2)设M(0,-1),若斜率为k(k≠0)的直线l与P点的轨迹交于不同的两点A、B,若要使|MA|=|MB|,试求k的取值范围.
设F1、F2分别为椭圆C: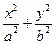 =1(a>b>0)的左、右焦点,过F2的直线l与椭圆C相交于A,B两点,直线l的倾斜角为60°,F1到直线l的距离为2
=1(a>b>0)的左、右焦点,过F2的直线l与椭圆C相交于A,B两点,直线l的倾斜角为60°,F1到直线l的距离为2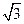 .
.
(1)求椭圆C的焦距;
(2)如果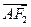 =2
=2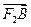 ,求椭圆C的方程.
,求椭圆C的方程.
在平面直角坐标系xOy中,直线l过抛物线y2=4x的焦点F交抛物线于A、B两点.
(1) 若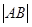 =8,求直线l的斜率
=8,求直线l的斜率
(2)若 =m,
=m,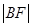 =n.求证
=n.求证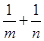 为定值
为定值
如图,矩形ABCD和梯形BEFC所在平面互相垂直,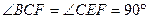 ,
,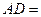
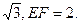
(1)求证: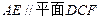 ;
;
(2)求证: ;
;
(3)当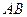 的长为何值时,二面角
的长为何值时,二面角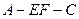 的大小为60°?
的大小为60°?
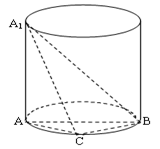
如图,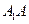 是圆柱的母线,
是圆柱的母线,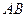 是圆柱底面圆的直径,
是圆柱底面圆的直径,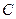 是底面圆周上异于
是底面圆周上异于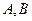 的任意一点,
的任意一点,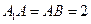 .(Ⅰ)求证:
.(Ⅰ)求证: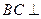 平面
平面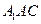 ;(Ⅱ)求三棱锥
;(Ⅱ)求三棱锥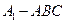 的体积的最大值.
的体积的最大值.