本题共有3个小题,第1小题满分4分,第2小题满分8分,
第3小题满分6分.
设 把三阶行列式
把三阶行列式 中第一行第二列元素的余子式记为
中第一行第二列元素的余子式记为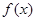 ,且关于
,且关于 的不等式
的不等式 的解集为
的解集为 。各项均为正数的数列
。各项均为正数的数列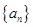 的前
的前 项和为
项和为 ,点列
,点列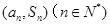 在函数
在函数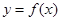 的图象上。
的图象上。
(1)求函数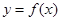 的解析式;
的解析式;
(2)若 ,求
,求 的值;
的值;
(3)令 ,求数列
,求数列 的前
的前 项中满足
项中满足 的所有项数之和.
的所有项数之和.
从某企业生产的某种产品中抽取20件,测量这些产品的一项质量指标值,由测量得到如图1的频率分布直方图,从左到右各组的频数依次记为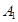 ,
,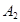 ,
,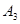 ,
,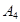 ,
,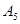 .
.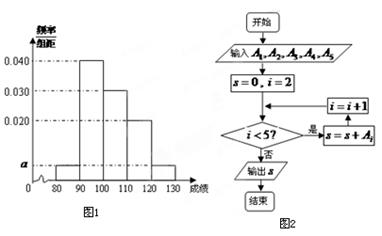
(1)求图1中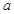 的值;
的值;
(2)图2是统计图1中各组频数的一个算法流程图,求输出的结果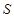 ;
;
(3)从质量指标值分布在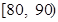 、
、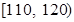 的产品中随机抽取2件产品,求所抽取两件产品的质量指标值之差大于10的概率.
的产品中随机抽取2件产品,求所抽取两件产品的质量指标值之差大于10的概率.
已知函数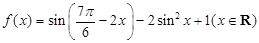 ,
,
(1)求函数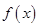 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;
(2)在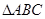 中,三内角
中,三内角 ,
,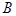 ,
,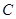 的对边分别为
的对边分别为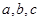 ,已知函数
,已知函数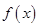 的图象
的图象
经过点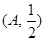 ,
,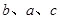 成等差数列,且
成等差数列,且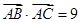 ,求
,求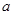 的值.
的值.
设函数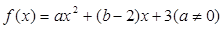 ,
,
(1)若不等式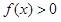 的解集
的解集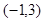 ,求
,求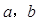 的值;
的值;
(2)若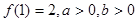 ,求
,求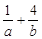 的最小值.
的最小值.
(本小题满分12分)设等比数列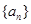 的前
的前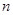 项和为
项和为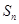 ,已知
,已知
(1)求数列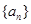 的通项公式;
的通项公式;
(2)在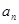 与
与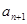 之间插入
之间插入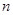 个数,使这
个数,使这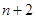 个数组成一个公差为
个数组成一个公差为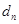 的等差数列,
的等差数列,
①在数列{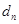 }中是否存在三项
}中是否存在三项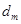 ,
,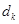 ,
,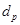 (其中
(其中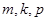 成等差数列)成等比数列?若存在,求出这样的三项,若不存在,说明理由;
成等差数列)成等比数列?若存在,求出这样的三项,若不存在,说明理由;
②记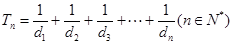 ,求满足
,求满足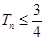 的
的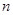 值.
值.
(本小题满分12分)如图,在平面直角坐标系内,已知 ,
, 两点,且圆
两点,且圆
的方程为 ,点
,点 为圆
为圆 上的动点.
上的动点.
(1)求过点 的圆的切线的方程;
的圆的切线的方程;
(2)求 的最大值及其对应的点
的最大值及其对应的点 的坐标.
的坐标.