(本小题满分12分)设等比数列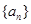 的前
的前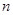 项和为
项和为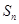 ,已知
,已知
(1)求数列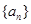 的通项公式;
的通项公式;
(2)在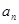 与
与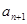 之间插入
之间插入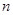 个数,使这
个数,使这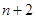 个数组成一个公差为
个数组成一个公差为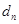 的等差数列,
的等差数列,
①在数列{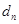 }中是否存在三项
}中是否存在三项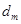 ,
,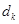 ,
,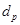 (其中
(其中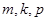 成等差数列)成等比数列?若存在,求出这样的三项,若不存在,说明理由;
成等差数列)成等比数列?若存在,求出这样的三项,若不存在,说明理由;
②记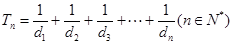 ,求满足
,求满足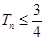 的
的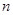 值.
值.
(本小题满分14分)已知四棱锥P—GBCD中(如图),PG⊥平面GBCD,GD∥BC,GD= BC,且BG⊥GC,GB=GC=2,E是BC的中点,PG=4
BC,且BG⊥GC,GB=GC=2,E是BC的中点,PG=4
(Ⅰ)求异面直线GE与PC所成角的余弦值;
(Ⅱ)若F点是棱PC上一点,且 ,
, ,求
,求 的值.
的值.
(本小题满分14分)已知正项数列 满足:
满足: ,
, 
(1)求通项 ;
;
(2)若数列 满足
满足 ,求数列
,求数列 的前
的前 项和.
项和.
设函数
(1)求函数 的周期和单调递增区间;
的周期和单调递增区间;
(2)设A,B,C为 ABC的三个内角,若AB=1,
ABC的三个内角,若AB=1,  ,
, ,求s1nB的值.
,求s1nB的值.
已知函数
(1)若曲线 在点
在点 处的切线与直线
处的切线与直线 平行,求
平行,求 的值;
的值;
(2)求证函数 在
在 上为单调增函数;
上为单调增函数;
(3)设 ,
, ,且
,且 ,求证:
,求证: .
.
已知椭圆C: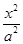 +
+ =1
=1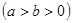 的离心率为
的离心率为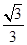 ,左焦点为F(-1,0),
,左焦点为F(-1,0),
(1)设A,B分别为椭圆的左、右顶点,过点F且斜率为k的直线L与椭圆C交于M,N两点,若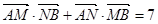 ,求直线L的方程;
,求直线L的方程;
(2)椭圆C上是否存在三点P,E,G,使得S△OPE=S△OPG=S△OEG= ?
?