已知椭圆C: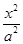 +
+ =1
=1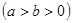 的离心率为
的离心率为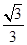 ,左焦点为F(-1,0),
,左焦点为F(-1,0),
(1)设A,B分别为椭圆的左、右顶点,过点F且斜率为k的直线L与椭圆C交于M,N两点,若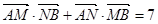 ,求直线L的方程;
,求直线L的方程;
(2)椭圆C上是否存在三点P,E,G,使得S△OPE=S△OPG=S△OEG= ?
?
在
中,内角
的对边分别为
.已知
,
.
(1)求
的值;
(2)若
,求
的面积.
已知
,函数
.
(Ⅰ)证明:当
时,
(ⅰ)函数
的最大值为
;
(ⅱ)
;
(Ⅱ) 若
对
[0,1]恒成立,求
的取值范围.
如图,椭圆
的离心率为
,其左焦点到点
的距离为
.不过原点
的直线
与
相交于
两点,且线段
被直线
平分.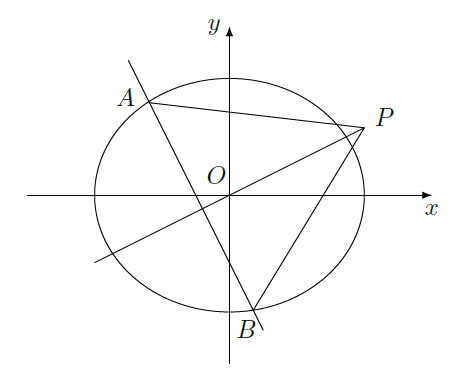
(Ⅰ)求椭圆
的方程;
(Ⅱ) 求
的面积取最大时直线
的方程.
如图,在四棱锥
中,底面是边长为
的菱形,且
,且
平面
,
,
分别为
的中点.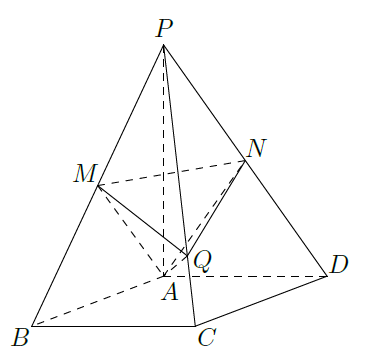
(1)证明:
平面
;
(2) 过点
作
,垂足为点
,求二面角
的平面角的余弦值.
已知箱中装有4个白球和5个黑球,且规定:取出一个白球的2分,取出一个黑球的1分.现从该箱中任取(无放回,且每球取到的机会均等)3个球,记随机变量
为取出3球所得分数之和.
(Ⅰ)求
的分布列;
(Ⅱ)求
的数学期望
.