已知△ABC中, .
.
(I)求∠C的大小;
(Ⅱ)设角A,B,C的对边依次为 ,若
,若 ,且△ABC是锐角三角形,求
,且△ABC是锐角三角形,求 的取值范围.
的取值范围.
已知函数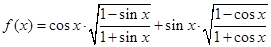
(1)求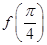 的值;(2)写出函数在
的值;(2)写出函数在 上的单调区间和值域。
上的单调区间和值域。
(本小题满分10分)选修4—5:不等式选讲
设函数 ,
,
(Ⅰ)若 ,解不等式
,解不等式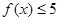 ;
;
(Ⅱ)若函数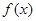 有最小值,求实数
有最小值,求实数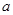 的取值范围.
的取值范围.
(本小题满分10分)选修4-4:坐标系与参数方程
已知极坐标系的极点与直角坐标系的原点重合,极轴与直角坐标系 轴的正半轴重合.直线的参数方程是
轴的正半轴重合.直线的参数方程是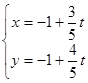 (
( 为参数),曲线
为参数),曲线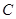 的极坐标方程为
的极坐标方程为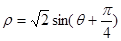 .
.
(Ⅰ)求曲线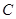 的直角坐标方程;(Ⅱ)设直线与曲线
的直角坐标方程;(Ⅱ)设直线与曲线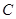 相交于
相交于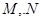 两点,求
两点,求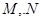 两点间的距离.
两点间的距离.
设函数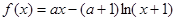 ..
..
(Ⅰ)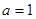 时,求
时,求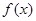 的单调区间;
的单调区间;
(Ⅱ)当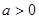 时,设
时,设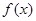 的最小值为
的最小值为 ,若
,若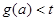 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.