本题共有2个小题,第1小题满分6分,第2小题满分6分.
已知复数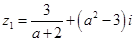 ,
,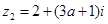 (
( ,
,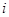 是虚数单位)。
是虚数单位)。
(1)若复数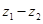 在复平面上对应点落在第一象限,求实数
在复平面上对应点落在第一象限,求实数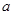 的取值范围
的取值范围
(2)若虚数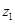 是实系数一元二次方程
是实系数一元二次方程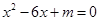 的根,求实数
的根,求实数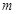 的值.
的值.
直三棱柱
中,
.
(Ⅰ)证明
;
(Ⅱ)已知
,求三棱锥
的体积.
函数
的最大值为3, 其图像相邻两条对称轴之间的距离为
,
(1)求函数
的解析式;
(2)设
,则
,求
的值
已知等比数列
的公比为
.
(1)若
= ,求数列
的前
项和;
,求数列
的前
项和;
(Ⅱ)证明:对任意
,
,
,
成等差数列.
已知
为正实数,
为自然数,抛物线
与
轴正半轴相交于点
,设
为该抛物线在点
处的切线在
轴上的截距.
(1)用
和
表示
;
(2)求对所有
都有
成立的
的最小值;
(3)当
时,比较
与
的大小,并说明理由.
如图,动点 到两定点 、 构成 ,且 ,设动点 的轨迹为 .
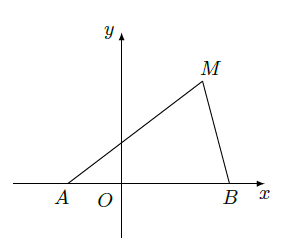
(Ⅰ)求轨迹
的方程;
(Ⅱ)设直线
与
轴交于点
,与轨迹
相交于点
、
,且
,求
的取值范围。