已知
为正实数,
为自然数,抛物线
与
轴正半轴相交于点
,设
为该抛物线在点
处的切线在
轴上的截距.
(1)用
和
表示
;
(2)求对所有
都有
成立的
的最小值;
(3)当
时,比较
与
的大小,并说明理由.
(本小题满分13分)已知直线 经过点A
经过点A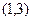 ,求:
,求:
(1)直线 在两坐标轴上的截距相等的直线方程;
在两坐标轴上的截距相等的直线方程;
(2)直线 与两坐标轴的正向围成三角形面积最小时的直线方程;
与两坐标轴的正向围成三角形面积最小时的直线方程;
(3)求圆 关于直线OA对称的圆的方程。
关于直线OA对称的圆的方程。
(本小题满分13分)某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出。当每辆车的月租金每增加50元时,未租出的车将会增加一辆。租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元。
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
(本小题满分13分)已知函数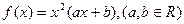 在
在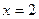 时有极值,其图象在点
时有极值,其图象在点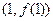 处的切线与直线
处的切线与直线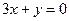 平行.
平行.
(1)求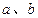 的值和函数
的值和函数 的单调区间;
的单调区间;
(2)若当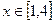 时,恒有
时,恒有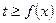 ,试确定
,试确定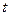 的取值范围.
的取值范围.
(本小题满分13分)设集合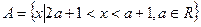 ,
, ,若
,若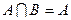 。求实数a的取值范围。
。求实数a的取值范围。
已知函数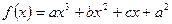 (
(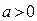 )的单调递减区间是
)的单调递减区间是 ,且满足
,且满足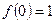 .
.
(Ⅰ)求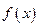 的解析式;
的解析式;
(Ⅱ)对任意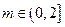 , 关于
, 关于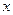 的不等式
的不等式 在
在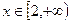 上有解,求实数
上有解,求实数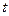 的取值范围.
的取值范围.