本题共有2个小题,第1小题满分8分,第2小题满分6分.
为保护环境,某单位采用新工艺,把二氧化碳转化为一种可利用的化工产品。已知该单位每月的处理量最多不超过300吨,月处理成本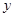 (元)与月处理量
(元)与月处理量 (吨)之间的函数关系式可近似的表示为:
(吨)之间的函数关系式可近似的表示为: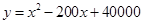 ,且每处理一吨二氧化碳得到可利用的化工产品价值为300元。
,且每处理一吨二氧化碳得到可利用的化工产品价值为300元。
(1)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?
(2)要保证该单位每月不亏损,则每月处理量应控制在什么范围?
的内角
所对的边分别为
,向量
与
平行.
(Ⅰ)求
;
(Ⅱ)若
,求
的面积.
已知关于
的不等式
的解集为
.
(Ⅰ)求实数
的值;
(Ⅱ)求
的最大值.
在直角坐标系 中,直线 的参数方程为 ( 为参数).以原点为极点, 轴正半轴为极轴建立极坐标系. 的极坐标方程为 .
(Ⅰ)写出 的直角坐标方程;
(Ⅱ) 为直线 上一动点,当 到圆心 的距离最小时,求 的直角坐标.
如图,
切
于点 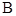 ,直线
交
于
,
,直线
交
于
, 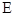 两点,
,垂足为
.
两点,
,垂足为
.
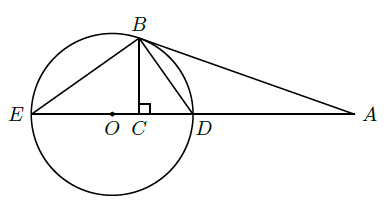
(Ⅰ)证明:
;
(Ⅱ)若
,
,求
的直径.
设
是等比数列 ,
,的各项和,其中
,
,
,的各项和,其中
,
(Ⅰ)证明:函数
在
内有且仅有一个零点(记为
),且
;
(Ⅱ)设有一个与上述等比数列的首项、末项、项数分别相同的等差数列,其各项和为
,比较
与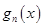 的大小,并加以证明.
的大小,并加以证明.