在直角坐标系中,直线的参数方程为(为参数).以原点为极点,轴正半轴为极轴建立极坐标系.的极坐标方程为.
(Ⅰ)写出的直角坐标方程;
(Ⅱ)为直线上一动点,当到圆心的距离最小时,求的直角坐标.
(本小题满分14分)设圆 ,将曲线上每一点的纵坐标压缩到原来的
,将曲线上每一点的纵坐标压缩到原来的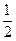 ,对应的横坐标不变,得到曲线C.经过点M(2,1),平行于OM的直线
,对应的横坐标不变,得到曲线C.经过点M(2,1),平行于OM的直线 在y轴上的截距为m(m≠0),
在y轴上的截距为m(m≠0), 交曲线C于A、B两个不同点.
交曲线C于A、B两个不同点.
(1)求曲线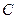 的方程;
的方程;
(2)求m的取值范围;
(3)求证直线MA、MB与x轴始终围成一个等腰三角形.
(本小题满分14分)已知公差大于零的等差数列{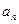 }的前n项和为
}的前n项和为 ,且满足
,且满足 ,
, .
. ⑴求通项
⑴求通项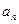 ;
;
⑵若数列
 是等差数列,且
是等差数列,且 ,求非零常数c;
,求非零常数c;
⑶比较 (
(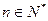 )的大小.
)的大小.
19.(本小题满分14分)设有关于 的一元二次
的一元二次
方程 .
.
(Ⅰ)若 是从
是从 四个数中任取的一个数,
四个数中任取的一个数, 是从
是从 三个数中任取的一个数,求上述方程有实根的概率;
三个数中任取的一个数,求上述方程有实根的概率;
(Ⅱ)若 是从区间
是从区间 任取的一个数,
任取的一个数, 是从区间
是从区间 任取的一个数,求上述方程有实根的概率.
任取的一个数,求上述方程有实根的概率.
(本小题满分14分)如图,已知四棱锥P-ABCD中,PA⊥平面CDAB, ABCD是直角梯形,AD∥BC,∠BAD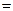 90º,BC
90º,BC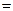 2,PA
2,PA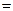 AB
AB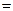 1.
1.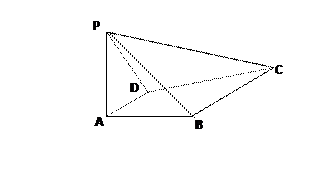
(1)求证:PD⊥AB;
(2)在线段PB上找一点E,使AE//平面PCD;
(3)求点D到平面PBC的距离.
(本小题满分12分)已知函数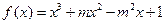 (m为常数,且m>0)有极大值9.
(m为常数,且m>0)有极大值9.
(Ⅰ)求m的值;
(Ⅱ)若斜率为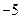 的直线是曲线
的直线是曲线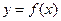 的切线,求此直线方程.
的切线,求此直线方程.