中央电视台《同一首歌》大型演唱会曾在厦门举行,之前甲、乙两人参加大会青年志愿者的选拔.已知在备选的10道试题中,甲能答对其中的6题,乙能答对其中的8题。规定每次考试都从备选题中随机抽出3题进行测试,至少答对2题才能入选。
(Ⅰ)求甲答对试题数ξ的概率分布 (列表);
(列表);
(Ⅱ)求甲、乙两人至少有一人入选的概率。
如图,在斜三棱柱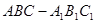 中,点
中,点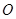 、
、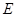 分别是
分别是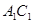 、
、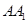 的中点,
的中点,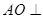 平面
平面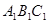 .已知
.已知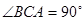 ,
,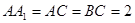 .
.
(Ⅰ)证明: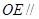 平面
平面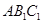 ;
;
(Ⅱ)求异面直线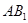 与
与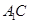 所成的角;
所成的角;
(Ⅲ)求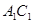 与平面
与平面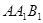 所成角的正弦值.
所成角的正弦值.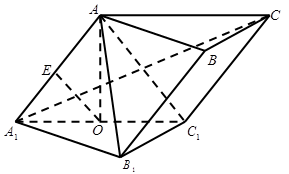
一个口袋内有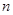 (
(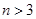 )个大小相同的球,其中有3个红球和
)个大小相同的球,其中有3个红球和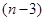 个白球.已知从口袋中随机取出一个球是红球的概率是
个白球.已知从口袋中随机取出一个球是红球的概率是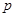 .
.
(I)当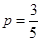 时,不放回地从口袋中随机取出3个球,求取到白球的个数
时,不放回地从口袋中随机取出3个球,求取到白球的个数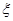 的期望
的期望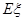 ;
;
(II)若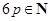 ,有放回地从口袋中连续地取四次球(每次只取一个球),在四次摸球中恰好取到两次红球的概率大于
,有放回地从口袋中连续地取四次球(每次只取一个球),在四次摸球中恰好取到两次红球的概率大于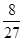 ,求
,求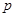 和
和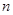 .
.
数列 中,
中, (
( ,),且
,),且 成公比不为1的等比数列.
成公比不为1的等比数列.
(1) 求 的值;
的值;
(2)求 的通项公式.
的通项公式.
(3) 求数列 的前
的前 项和
项和 .
.
已知数列 的前
的前 项和,
项和, 。
。
(1)求数列 的通项公式
的通项公式 ;
;
(2)记 ,求
,求
设不等式 的解集为A,不等式
的解集为A,不等式 的解集为B.
的解集为B.
(1)求A∩B;
(2)若不等式 的解集为A∩B,求
的解集为A∩B,求 的值.
的值.