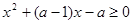一个口袋内有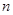 (
(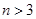 )个大小相同的球,其中有3个红球和
)个大小相同的球,其中有3个红球和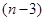 个白球.已知从口袋中随机取出一个球是红球的概率是
个白球.已知从口袋中随机取出一个球是红球的概率是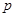 .
.
(I)当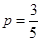 时,不放回地从口袋中随机取出3个球,求取到白球的个数
时,不放回地从口袋中随机取出3个球,求取到白球的个数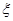 的期望
的期望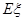 ;
;
(II)若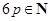 ,有放回地从口袋中连续地取四次球(每次只取一个球),在四次摸球中恰好取到两次红球的概率大于
,有放回地从口袋中连续地取四次球(每次只取一个球),在四次摸球中恰好取到两次红球的概率大于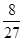 ,求
,求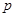 和
和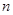 .
.
在数列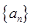 中,对于任意
中,对于任意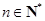 ,等式:
,等式: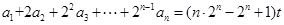 恒成立,其中常数
恒成立,其中常数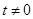 .
.
(1)求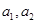 的值;(2)求证:数列
的值;(2)求证:数列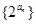 为等比数列;
为等比数列;
(3)如果关于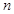 的不等式
的不等式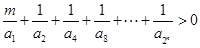 的解集为
的解集为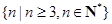 ,试求实数
,试求实数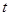 、
、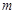 的取值范围.
的取值范围.
作为绍兴市2013年5.1劳动节系列活动之一的花卉展在镜湖湿地公园举行.现有一占地1800平方米的矩形地块,中间三个矩形设计为花圃(如图),种植有不同品种的观赏花卉,周围则均是宽为1米的赏花小径,设花圃占地面积为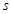 平方米,矩形一边的长为
平方米,矩形一边的长为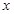 米(如图所示)
米(如图所示)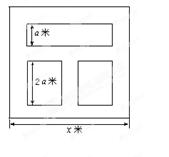
(1)试将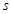 表示为
表示为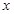 的函数;
的函数;
(2)问应该如何设计矩形地块的边长,使花圃占地面积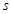 取得最大值.
取得最大值.
在等比数列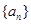 中,已知
中,已知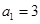 ,公比
,公比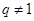 ,等差数列
,等差数列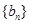 满足
满足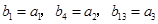 .
.
(Ⅰ)求数列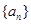 与
与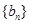 的通项公式;
的通项公式;
(Ⅱ)记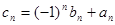 ,求数列
,求数列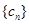 的前2n项和.
的前2n项和.
在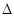
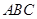 中,内角
中,内角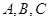 的对边分别为
的对边分别为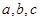 .已知
.已知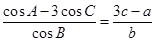 .
.
(Ⅰ)求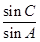 的值;
的值;
(Ⅱ)若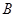 为钝角,
为钝角,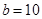 ,求
,求 的取值范围.
的取值范围.
已知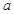 是实数,试解关于
是实数,试解关于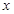 的不等式:
的不等式: