(本小题满分12分)
从装有2只红球,2只白球和1只黑球的袋中逐一取球,已知每只球被抽取的可能性相同。
(1)若抽取后又放回,抽3次,分别求恰2次为红球的概率及抽全三种颜色球的概率;
(2)若抽取后不放回,求抽完红球所需次数不少于4次的概率。
(本小题满分10分)
已知集合 ,
,
(1)当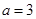 时,求
时,求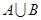 ;
;
(2)若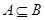 ,求实数
,求实数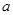 的取值范围。
的取值范围。
(本小题满分12分)
已知 对于任意实数
对于任意实数 满足
满足 ,当
,当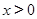 时,
时,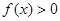 .
.
(1)求 并判断
并判断 的奇偶性;
的奇偶性;
(2)判断 的单调性,并用定义加以证明;
的单调性,并用定义加以证明;
(3)已知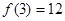 ,集合
,集合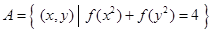 ,
,
集合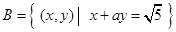 ,若
,若 ,求实数
,求实数 的取值范围.
的取值范围.
(本小题满分12分)
已知 令
令 .
.
(1)求 的表达式;
的表达式;
(2)若函数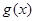 和函数
和函数 的图象关于原点对称,
的图象关于原点对称,
(ⅰ)求函数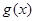 的解析式;
的解析式;
(ⅱ)若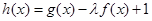 在区间
在区间 上是增函数,求实数l的取值范围.
上是增函数,求实数l的取值范围.
(本小题满分12分)
已知圆C: .
.
(1)若圆C的切线在x轴和y轴上的截距相等,求此切线的方程;
(2)从圆C外一点P(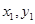 )向该圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使得|PM|取得最小值的点P的坐标.
)向该圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使得|PM|取得最小值的点P的坐标.
(本小题满分12分)
如图,菱形ABCD与矩形BDEF所在平面互相垂直, .
.
(1)求证:FC∥平面AED;
(2)若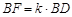 ,当二面角
,当二面角 为直二面角时,求k的值.
为直二面角时,求k的值.