(满分12分)直线l 与抛物线y2 = 4x 交于两点A、B,O 为原点,且 = -4.
= -4.
(I) 求证:直线l 恒过一定点;
(II) 若 4 ≤| AB | ≤
≤| AB | ≤ ,求直线l 的
,求直线l 的 斜率k 的取值范围;
斜率k 的取值范围;
(Ⅲ) 设抛物线的焦点为F,∠AFB = θ,试问θ 角 能否
能否 等于120°?若能,求出相应的直线l 的方程;若不能,请说明理由.
等于120°?若能,求出相应的直线l 的方程;若不能,请说明理由.
(本小题满分10分)某港口的水深 (米)是时间
(米)是时间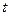 (
( ,单位:小时)的函数,下面是每天时间与水深的关系表:
,单位:小时)的函数,下面是每天时间与水深的关系表:
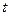 |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
 |
10 |
13 |
9.9 |
7 |
10 |
13 |
10.1 |
7 |
10 |
经过长期观测,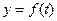 可近似的看成是函数
可近似的看成是函数
(1)根据以上数据,求出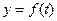 的解析式
的解析式
(2)若船舶航行时,水深至少要11.5米才是安全的,那么船舶在一天中的哪几段时间可以安全的进出该港?
(本小题满分8分)已知 ,
, ,当
,当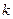 为何值时,
为何值时,
(1)  与
与 垂直?
垂直?
(2)  与
与 平行?平行时它们是同向还是反向?
平行?平行时它们是同向还是反向?
(满分8分)已知的值.
(本小题满分8分)已知向量 ,
,  的夹角为
的夹角为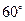 , 且
, 且 ,
,  ,
,
(1) 求 ; (2) 求
; (2) 求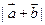 .
.
(本小题满分8分)
(1)已知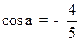 ,且
,且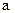 为第三象限角,求
为第三象限角,求 的值
的值
(2)已知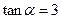 ,计算
,计算 的值
的值