数列 的首项为
的首项为 ,前n项和为
,前n项和为 ,且
,且 ,设
,设 ,cn=k+b1+b2+…+bn(k∈R+).
,cn=k+b1+b2+…+bn(k∈R+).
(1)求数列{an}的通项公式;
(2)当t=1时,若对任意n∈N*,|bn|≥|b3|恒成立,求a的取值范围;
(3)当t≠1时,试求三个正数a,t,k的一组值,使得{cn}为等比数列,且a,t,k成等差数列.
(本题共2小题,满分14分。第1小题满分6分,第2小题满分8分)
提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度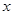 (单位:辆/千米)的函数.当桥上的车流密度达到
(单位:辆/千米)的函数.当桥上的车流密度达到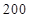 辆/千米时,造成堵塞,此时车流速度为
辆/千米时,造成堵塞,此时车流速度为 千米/小时;当车流密度不超过
千米/小时;当车流密度不超过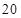 辆/千米时,车流速度为
辆/千米时,车流速度为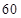 千米/小时,研究表明;当
千米/小时,研究表明;当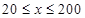 时,车流速度
时,车流速度 是车流密度
是车流密度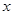 的一次函数.
的一次函数.
(1)求函数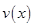 的表达式;
的表达式;
(2)当车流密度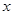 为多大时,车流量(单位时间内通过桥上某一点的车辆数,单位:辆/每小时)
为多大时,车流量(单位时间内通过桥上某一点的车辆数,单位:辆/每小时) 可以达到最大,并求出最大值(精确到1辆/小时).
可以达到最大,并求出最大值(精确到1辆/小时).
(本题共2小题,满分14分。第1小题满分7分,第2小题满分7分)
定义: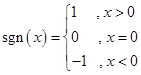 ,若已知函数
,若已知函数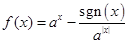 (
(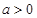 且
且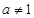 )满足
)满足 .
.
(1)解不等式: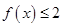 ;
;
(2)若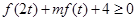 对于任意正实数
对于任意正实数 恒成立,求实数
恒成立,求实数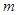 的取值范围.
的取值范围.
(本题共2小题,满分12分。第1小题满分6分,第2小题满分6分)
已知复数 ,
,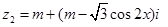 (
( ),且
),且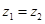 .
.
(1)设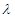 =
=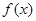 ,求
,求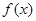 的最小正周期和单调递增区间.
的最小正周期和单调递增区间.
(2)当 时,求函数
时,求函数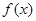 的值域.
的值域.
已知函数


⑴试就实数 的不同取值,写出该函数的单调递增区间;
的不同取值,写出该函数的单调递增区间;
⑵已知当 时,函数在
时,函数在 上单调递减,在
上单调递减,在 上单调递增,求
上单调递增,求 的值并写出函数的解析式;
的值并写出函数的解析式;
⑶若函数 在区间
在区间 内有反函数,试求出实数
内有反函数,试求出实数 的取值范围。
的取值范围。
我国加入WTO时,据达成的协议,若干年内某产品关税与市场供应量 的关系允许近似满足
的关系允许近似满足 (其中,
(其中, 为关税的税率,且
为关税的税率,且 ,
, 为市场价格,
为市场价格, 、
、 为正常数),当
为正常数),当 时,市场供应量曲线如图:
时,市场供应量曲线如图:
⑴根据图象求 的值;
的值;
⑵记市场需求量为 ,它近似满足
,它近似满足 ,当
,当 时,市场价格称为市场平衡价格,当市场平衡价
时,市场价格称为市场平衡价格,当市场平衡价 时,求税率的最小值。
时,求税率的最小值。