探究函数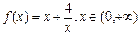
的最小值，并确定取得最小值时x的值。列表如下：
| x |
… |
0.5 |
1 |
1.5 |
1.7 |
1.9 |
2 |
2.1 |
2.2 |
2.3 |
3 |
4 |
5 |
7 |
… |
| y |
… |
8.5 |
5 |
4.17 |
4.05 |
4.005 |
4 |
4.005 |
4.02 |
4.04 |
4.3 |
5 |
5.8 |
7.57 |
… |
请观察表中y值随x值变化的特点，完成以下的问题。
(1)函数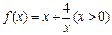
在区间（0，2）上递减，在区间 上递增。当
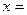时，
。
(2)证明：函数
在区间（0，2）递减。
(3)思考：函数
时有最值吗？是最大值还是最小值？此时
x为何值？（直接回答结果，不需证明）
(本小题12分)
一个多面体如图所示，四边形ABCD是边长为2的正方形，AB=FB，FB⊥平面ABCD，
ED∥FB，且ED=1。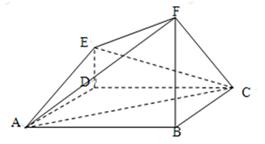
1） 求证：平面ACE⊥平面ACF。
2） 求多面体AED-BCF的体积。
(本小题10分)
我校在筹办元旦艺术节前，对学生是喜欢曲艺还是舞蹈节目做了一次调查，随机抽取了100名学生，相关数据如下表所示
1） 若从喜欢舞蹈节目的45名学生中按性别分层随机抽取5名，则女生应该抽取几名；
2） 在1）中抽取的5名学生中任取2名，求恰好有1名男生的概率。
（本小题12分）
已知数列{an}的前n项和为Sn，且满足an＋2SnSn-1=0(n≥2,n∈N)，a1=
。
1) 求证：数列{
}为等差数列。并求数列{an}的通项公式an。
2) 记数列{bn}的通项公式为bn=
,Tn=b1＋b2 ＋…＋bn,求Tn的值。
（本小题10分）
已知函数f(x)=cos(
－2x)＋2cos2x
1)求f(x)的最大值，并写出使f(x)取得最大值时对应的x的集合.
2)若把函数f(x)的图象向右平移
个单位长度后得到函数g(x)的图象，求函数g(x)的单调递减区间。
（本小题满分14分）
某地区有小学21所，中学14所，大学7所，现采用分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查．
（1）求应从小学、中学、大学中分别抽取的学校数目；
（2）若从抽取的6所学校中随机抽取2所学校做进一步数据分析．
（ⅰ）列出所有可能的抽取结果；
（ⅱ）求抽取的2所学校均为小学的概率．