(本小题10分)
我校在筹办元旦艺术节前,对学生是喜欢曲艺还是舞蹈节目做了一次调查,随机抽取了100名学生,相关数据如下表所示
1) 若从喜欢舞蹈节目的45名学生中按性别分层随机抽取5名,则女生应该抽取几名;
2) 在1)中抽取的5名学生中任取2名,求恰好有1名男生的概率。
若 的展开式中只有第10项的二项式系数最大,
的展开式中只有第10项的二项式系数最大,
(1)求展开式中系数最大的项;
(2)设 ,求
,求 .
.
甲、乙两队在进行一场五局三胜制的排球比赛中,规定先赢三局的队获胜,并且比赛就此结束,现已知甲、乙两队每比赛一局,甲队获胜的概率为 ,乙队获胜的概率为
,乙队获胜的概率为 ,且每局比赛的胜负是相互独立的,问:
,且每局比赛的胜负是相互独立的,问:
(1)甲队以 获胜的概率是多少?
获胜的概率是多少?
(2)乙队获胜的概率是多少?
在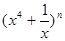 的展开式中,第三项的二项式系数比第二项的二项式系数大35。
的展开式中,第三项的二项式系数比第二项的二项式系数大35。
(1)求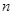 的值;(2)求展开式中的常数项。
的值;(2)求展开式中的常数项。
已知数列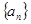 的前
的前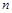 项和
项和 是二项式
是二项式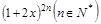 展开式中含
展开式中含 奇次幂的系数和.
奇次幂的系数和.
(1)求数列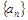 的通项公式;
的通项公式;
(2)设 ,求
,求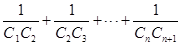 的值.
的值.
在平面直角坐标系 中,动点
中,动点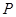 到两点
到两点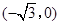 ,
,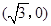 的距离之和等于
的距离之和等于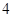 ,设点
,设点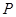 的轨迹为曲线
的轨迹为曲线 ,直线
,直线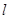 过点
过点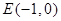 且与曲线
且与曲线 交于
交于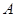 ,
,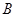 两点.
两点.
(1)求曲线 的轨迹方程;
的轨迹方程;
(2)是否存在△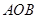 面积的最大值,若存在,求出△
面积的最大值,若存在,求出△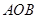 的面积;若不存在,说明理由.
的面积;若不存在,说明理由.