(本小题满分12分)如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,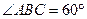 ,E,F分别是BC, PC的中点.
,E,F分别是BC, PC的中点.
(1)证明:AE⊥PD;
(2)若H为PD上的动点,EH与平面PAD所成最大角的正切值为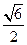 ,求二面角E—AF—C的余弦值.
,求二面角E—AF—C的余弦值.
已知函数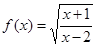 的定义域为集合A,函数
的定义域为集合A,函数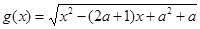 的定义域为集合B.
的定义域为集合B.
(1)求集合A、B;
(2)若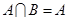 ,求实数
,求实数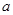 的取值范围.
的取值范围.
已知函数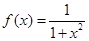 .
.
(1)求 的值;
的值;
(2)求 的值域.
的值域.
设集合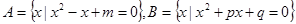 ,且
,且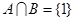 ,
,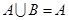 .
.
(1)求实数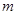 的值;
的值;
(2)求实数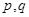 的值.
的值.
已知函数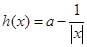 ,
,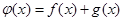 ,其中
,其中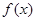 是
是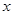 的正比例函数,
的正比例函数, 是
是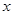 的反比例函数,且
的反比例函数,且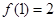 ,
,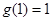 .
.
(1)求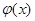 的解析式,并指出定义域;
的解析式,并指出定义域;
(2)求证:函数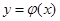 在
在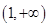 上是增函数;
上是增函数;
(3)若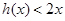 在
在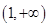 上恒成立,求实数
上恒成立,求实数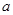 的取值范围.
的取值范围.
《中华人民共和国个人所得税法》中规定:公民月工资所得不超过3500元的部分不必纳税,超过3500元的部分为全月应纳税所得额,即全月应纳税所得额=当月工资-3500元.个人所得税款按下表累加计算:
| 全月应纳税所得额 |
税率 |
| 不超过1500元 |
3% |
| 超过1500元至4500元的部分 |
10% |
| 超过4500元至9000元的部分 |
20% |
| …… |
…… |
【例如:某人某月工资为5500元,需交个人所得税为:(5500-3500-1500) 10%+1500
10%+1500 3%=95元】
3%=95元】
(1)求月工资为4200元应交的个人所得税款;
(2)设小明的月工资为 元
元 ,应交的个人所得税款为
,应交的个人所得税款为 元,求
元,求 与
与 之间的函数关系式;
之间的函数关系式;
(3)若小明今年3月份的工资应交个人所得税款145元,求他今年3月份工资.