(本小题满分12分)如图,棱柱ABCD—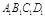 的底面
的底面 为菱 形 ,AC∩BD=O侧棱
为菱 形 ,AC∩BD=O侧棱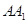 ⊥BD,点F为
⊥BD,点F为 的中点.
的中点.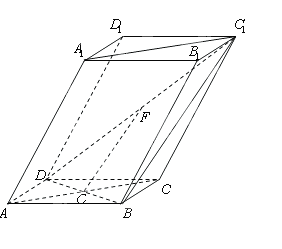
(Ⅰ)证明: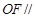 平面
平面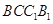 ;
;
(Ⅱ)证明:平面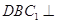 平面
平面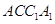 .
.
某校设计了一个实验学科的实验考查方案:考生从6道备选题中一次性随机抽取3题,按照题目要求独立完成全部实验操作.规定:至少正确完成其中2题的便可提高通过.已知6道备选题中考生甲有4题能正确完成,2题不能完成;考生乙每题正确完成的概率都是,且每题正确完成与否互不影响.分别写出甲、乙两考生正确完成题数的概率分布列;
设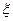 是一个离散型随机变量,其分布列如下表,求
是一个离散型随机变量,其分布列如下表,求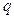 的值
的值
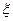 |
-1 |
0 |
1 |
| P |
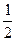 |
1-2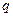 |
一个盒子装有六张卡片,上面分别写着如下六个定义域为R的函数: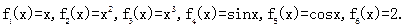 现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数的卡片则停止抽取,否则继续进行,求抽取次数
现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数的卡片则停止抽取,否则继续进行,求抽取次数 的分布列.
的分布列.
旅游公司为3个旅游团提供4条旅游线路,每个旅游团任选其中一条.求选择甲线路旅游团数的分布列.
写出下列随机变量可能取的值,并说明随机变量所取的值表示的随机试验的结果
(1)一袋中装有5只同样大小的白球,编号为1,2,3,4,5 现从该袋内随机取出3只球,被取出的球的最大号码数ξ;
现从该袋内随机取出3只球,被取出的球的最大号码数ξ;
(2)某单位的某部电话在单位时间内收到的呼叫次数η