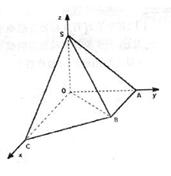
如图直角梯形OABC中, ,SO=1,以OC、OA、OS分别为x轴、y轴、z轴建立直角坐标系O-xyz.
,SO=1,以OC、OA、OS分别为x轴、y轴、z轴建立直角坐标系O-xyz.
(Ⅰ)求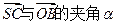 的大小(用反三角函数表示);
的大小(用反三角函数表示);
(Ⅱ)设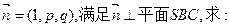
①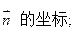
②OA与平面SBC的夹角 (用反三角函数表示);
(用反三角函数表示);
③O到平面SBC的距离.
(Ⅲ)设
① .
.
②异面直线SC、OB的距离为 .
(注:(Ⅲ)只要求写出答案).
在直角坐标系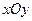 中,以原点
中,以原点 为极点,以
为极点,以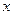 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线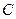 的极坐标方程为
的极坐标方程为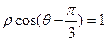 ,
,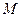 、
、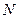 分别为
分别为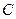 与
与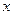 轴,
轴,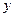 轴的交点,
轴的交点,
(1)写出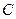 的直角坐标方程,并求
的直角坐标方程,并求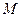 、
、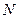 的极坐标;
的极坐标;
(2)设 的中点为
的中点为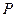 ,求直
,求直 线
线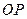 的极坐标方程.
的极坐标方程.
在医学生物学试验中,经常以果蝇作为试验对象,一个关有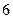 只果蝇的笼子里,不慎混入两只苍蝇(此时笼内共
只果蝇的笼子里,不慎混入两只苍蝇(此时笼内共 有
有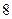 只蝇子:
只蝇子: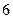 只果蝇和
只果蝇和 只苍蝇),只好把笼子打开一个小孔,让蝇子一只一只地往外飞,直到两只苍蝇都飞出,再关闭小孔,以
只苍蝇),只好把笼子打开一个小孔,让蝇子一只一只地往外飞,直到两只苍蝇都飞出,再关闭小孔,以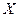 表示笼内还剩下的果蝇的只数;
表示笼内还剩下的果蝇的只数;
(1)写出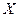 的分布列(不要求写出计算过程)
的分布列(不要求写出计算过程)
(2)求数学期望 ;
;
(3)求概率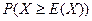 .
.
.
(1) 人坐在有八个座位的一排上,若每人的左右两边都要有空位,则不同的坐法的种数为几种?
人坐在有八个座位的一排上,若每人的左右两边都要有空位,则不同的坐法的种数为几种?
(2)甲、乙、丙 人站在共有
人站在共有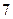 级的台阶上,若每级台阶最多站
级的台阶上,若每级台阶最多站 人,同一级台阶上
人,同一级台阶上
不区分站的位置,则有多少种不同的站法?
(3)现有 个保送大学的名额,分配给
个保送大学的名额,分配给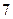 所学校,每校
所学校,每校 至少
至少 个名额,问名额分配的方法共有多少种?
个名额,问名额分配的方法共有多少种?
在直角坐标系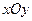 中,直线
中,直线 的参数方程为
的参数方程为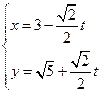 (
( 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系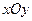 取相同的长度单位且以原点
取相同的长度单位且以原点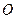 为极点,以
为极点,以 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆 的方程为
的方程为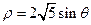 ,
,
(1)求圆 的直角坐标方程;
的直角坐标方程;
(2)设圆 与直线
与直线 交于点
交于点 、
、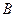 ,若
,若 的坐标为
的坐标为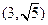 ,求
,求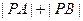 .
.
.已知 的展开式中,前三项的系数的绝对值依次成等差数列,
的展开式中,前三项的系数的绝对值依次成等差数列,
(1)证明:展开式中没有常数项;
(2)求展开式中所有有理项.