设关于x的方程sinx+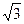 cosx+a=0在(0, 2π)内有相异二解α、β.
cosx+a=0在(0, 2π)内有相异二解α、β.
(Ⅰ)求α的取值范围; (Ⅱ)求tan(α+β)的值.
某产品的三个质量指标分别为x,y,z,用综合指标S=x+y+z评价该产品的等级.若S≤4,则该产品为一等品.先从一批该产品中,随机抽取10件产品作为样本,其质量指标列表如下:
| 产品编号 |
A1 |
A2 |
A3 |
A4 |
A5 |
| 质量指标(x,y,z) |
(1,1,2) |
(2,1,1) |
(2,2,2) |
(1,1,1) |
(1,2,1) |
| 产品编号 |
A6 |
A7 |
A8 |
A9 |
A10 |
| 质量指标(x,y,z) |
(1,2,2) |
(2,1,1) |
(2,2,1) |
(1,1,1) |
(2,1,2) |
(1)利用上表提供的样本数据估计该批产品的一等品率;
(2)在该样品的一等品中,随机抽取两件产品,
①用产品编号列出所有可能的结果;
②设事件B为“在取出的2件产品中,每件产品的综合指标S都等于4”,求事件B发生的概率.
在添加剂的搭配使用中,为了找到最佳的搭配方案,需要对各种不同的搭配方式作比较.在试制某种洗涤剂时,需要选用两种不同的添加剂.现有芳香度分别为1,2,3,4,5,6的六种添加剂可供选用.根据试验设计原理,通常首先要随机选取两种不同的添加剂进行搭配试验.用X表示所选用的两种不同的添加剂的芳香度之和.求所选用的两种不同的添加剂的芳香度之和等于6的概率.
袋内装有6个球,这些球依次被编号为1,2,3,…,6,设编号为n的球质量为n2-6n+12(单位:g),如果从这些球中不放回的任意取出2个球(不受重量、编号的影响),求取出的两球质量相等的概率.
某篮球运动员在最近几场大赛中罚球投篮的结果如下:
| 投篮次数n |
8 |
10 |
12 |
9 |
10 |
16 |
| 进球次数m |
6 |
8 |
9 |
7 |
7 |
12 |
| 进球频率m/n |
(1)计算表中进球的频率;
(2)这位运动员投篮一次,进球的概率是多少?
为了比较两种治疗失眠症的药(分别称为A药,B药)的疗效,随机地选取20位患者服用A药,20位患者服用B药,这40位患者在服用一段时间后,记录他们日平均增加的睡眠时间(单位:h).试验的观测结果如下:
服用A药的20位患者日平均增加的睡眠时间:
| 0.6 |
1.2 |
2.7 |
1.5 |
2.8 |
1.8 |
2.2 |
2.3 |
3.2 |
3.5 |
| 2.5 |
2.6 |
1.2 |
2.7 |
1.5 |
2.9 |
3.0 |
3.1 |
2.3 |
2.4 |
服用B药的20位患者日平均增加的睡眠时间:
| 3.2 |
1.7 |
1.9 |
0.8 |
0.9 |
2.4 |
1.2 |
2.6 |
1.3 |
1.4 |
| 1.6 |
0.5 |
1.8 |
0.6 |
2.1 |
1.1 |
2.5 |
1.2 |
2.7 |
0.5 |
(1) 分别计算两组数据的平均数,从计算结果看,哪种药的疗效更好?
(2) 根据两组数据完成下面茎叶图,从茎叶图看,哪种药的疗效更好?
| A药 |
B药 |
|
| 0. 1. 2. 3. |