袋内装有6个球,这些球依次被编号为1,2,3,…,6,设编号为n的球质量为n2-6n+12(单位:g),如果从这些球中不放回的任意取出2个球(不受重量、编号的影响),求取出的两球质量相等的概率.
如图,在长方体ABCD—A1B1C1D1中,AD=AA1=1,AB=2,E为AB的中点,F为CC1的中点.
(1)证明:B F//平面E CD1
(2)求二面角D1—EC—D的余弦值.
定义在 上奇函数
上奇函数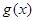 与偶函数
与偶函数 ,对任意
,对任意 满足
满足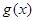 +
+
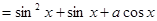 a为实数
a为实数
(1)求奇函数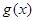 和偶函数
和偶函数 的表达式
的表达式
(2)若a>2, 求函数 在区间
在区间 上的最值
上的最值
(1) 已知直线(a+2)x+(1-a)y-3="0" 和直线(a-1)x +(2a+3)y+2="0" 互相垂直.求a值
(2) 求经过点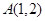 并且在两个坐标轴上的截距的绝对值相等的直线方程
并且在两个坐标轴上的截距的绝对值相等的直线方程
已知函数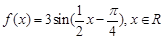 .
.
(1)列表并画出函数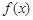 在长度为一个周期的闭区间上的简图;
在长度为一个周期的闭区间上的简图;
(2)将函数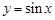 的图象作怎样的变换可得到
的图象作怎样的变换可得到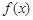 的图象?
的图象?
已知椭圆C: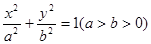 的两个焦点为F1、F2,点P在椭圆C上,且|PF1|=
的两个焦点为F1、F2,点P在椭圆C上,且|PF1|=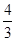 ,
,
|PF2|=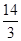 , PF1⊥F1F2.
, PF1⊥F1F2.
(1)求椭圆C的方程;(6分)
(2)若直线L过圆x2+y2+4x-2y=0的圆心M交椭圆于A、B两点,且A、B关于点M对称,求直线L的方程.