(本小题满分 分)某学校高三年级有学生1000名,经调查研究,其中750名同学经常参加体育锻炼(称为A类同学),另外250名同学不经常参加体育锻炼(称为B类同学),现用分层抽样方法(按A类、B类分二层)从该年级的学生中共抽查100名同学.
分)某学校高三年级有学生1000名,经调查研究,其中750名同学经常参加体育锻炼(称为A类同学),另外250名同学不经常参加体育锻炼(称为B类同学),现用分层抽样方法(按A类、B类分二层)从该年级的学生中共抽查100名同学.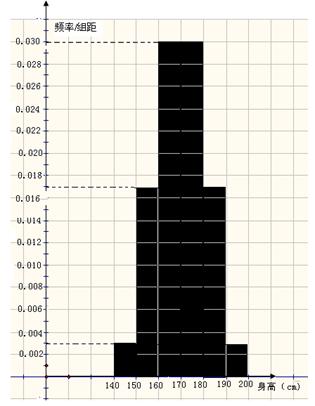
(Ⅰ)求甲、乙两同学都被抽到的概率,其中甲为A类同学,乙为B类同学;
(Ⅱ) 测得该年级所抽查的100名同学身高(单位:厘米) 频率分布直方图如右图:
(ⅰ) 统计方法中,同一组数据常用该组区间的中点值(例如区间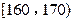 的中点值为165)作为代表.据此,计算这100名学生身高数据的期望
的中点值为165)作为代表.据此,计算这100名学生身高数据的期望 及标准差
及标准差 (精确到0.1);
(精确到0.1);
(ⅱ) 若总体服从正态分布,以样本估计总体,据此,估计该年级身高在 范围中的学生的人数.
范围中的学生的人数.
(Ⅲ) 如果以身高达170cm作为达标的标准,对抽取的100名学生,得到下列联表:
体育锻炼与身高达标2×2列联表
| |
身高达标 |
身高不达标 |
总计 |
| 积极参加体育锻炼 |
40 |
|
|
| 不积极参加体育锻炼 |
|
15 |
|
| 总计 |
|
|
100 |
(ⅰ)完成上表;
(ⅱ)请问有多大的把握认为体育锻炼与身高达标有关系?
参考公式:K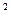 =
=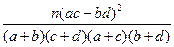 ,参考数据:
,参考数据:
P(K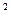 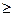 k) k) |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
| k |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
农科院的专家为了了解新培育的甲、乙两种麦苗的长势情况,从甲、乙两种麦苗的试验田中各抽取6株麦苗测量麦苗的株高,数据如下:(单位: )
)
甲:9,10,11,12,10,20
乙:8,14,13,10,12,21.
(1)在上面给出的方框内绘出所抽取的甲、乙两种麦苗株高的茎叶图;
(2)分别计算所抽取的甲、乙两种麦苗株高的平均数与方差,并由此判断甲、乙两种麦苗的长势情况.
已知一组数据的频率分布直方图如下.求众数、中位数、平均数.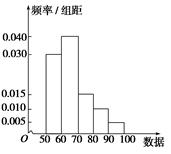
设计求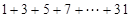 的算法,并画出相应的程序框图.
的算法,并画出相应的程序框图.
已知圆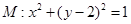 ,设点
,设点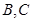 是直线
是直线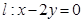 上的两点,它们的横坐标分别是
上的两点,它们的横坐标分别是 ,点
,点 在线段
在线段 上,过
上,过 点作圆
点作圆 的切线
的切线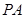 ,切点为
,切点为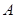 .
.
(1)若 ,求直线
,求直线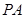 的方程;
的方程;
(2)经过 三点的圆的圆心是
三点的圆的圆心是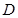 ,求线段
,求线段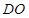 (
(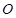 为坐标原点)长的最小值
为坐标原点)长的最小值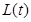 .
.
设函数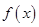 在定义域
在定义域 是奇函数,当
是奇函数,当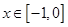 时,
时,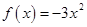 .
.
(1)当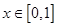 ,求
,求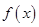 ;
;
(2)对任意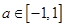 ,
,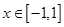 ,不等式
,不等式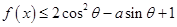 都成立,求
都成立,求 的取值范围.
的取值范围.