投掷一个质地均匀的、每个面上标有一个数字的正方体玩具,它的六个面中,有两个面标的数字是0,两个面标的数字是2,两个面标的数字是4,将此玩具连续抛掷两次,以两次朝上一面出的数字分别作为点P的横坐标和纵坐标。
(1)求点P落在区域C: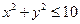 内的概率;
内的概率;
(2)若以落在区域C上的所有点为顶点作面积最大的多边形区域M,在区域C上随机撒一粒豆子,求豆子落在区域M上的概率。
如图,多面体ABC-A1B1C1中,三角形ABC是边长为4的正三角形,AA1∥BB1∥CC1,AA1⊥平面ABC,AA1=BB1=2CC1=4.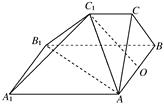
(1)若O是AB的中点,求证:OC1⊥A1B1;
(2)在线段AB1上是否存在一点D,使得CD∥平面A1B1C1,若存在,确定点D的位置;若不存在,请说明理由.
如图,三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°,E是棱CC1的中点,F是AB的中点,AC=BC=1,AA1=2.
(1)求证:CF∥平面AB1E;
(2)求三棱锥C-AB1E在底面AB1E上的高.
如图,已知四棱锥P-ABCD的底面为直角梯形,AB∥CD,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC= AB=1,M是PB的中点.
AB=1,M是PB的中点.
(1)求证:AM=CM;
(2)若N是PC的中点,求证:DN∥平面AMC.
如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°,已知PB=PD=2,PA= .
.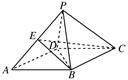
(1)证明:PC⊥BD;
(2)若E为PA的中点,求三棱锥P-BCE的体积.
如图,在三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC,AB⊥BC,O为AC中点.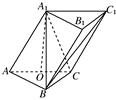
(1)证明:A1O⊥平面ABC;
(2)若E是线段A1B上一点,且满足VE-BCC1=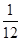 ·VABC-A1B1C1,求A1E的长度.
·VABC-A1B1C1,求A1E的长度.