某中学举办安全法规知识竞赛,从参赛的高一、高二学生中各抽出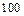 人的成绩作为样本.对高一年级的
人的成绩作为样本.对高一年级的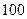 名学生的成绩进行统计,并按
名学生的成绩进行统计,并按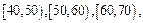
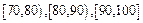 分组,得到成绩分布的频率分布直方图(如图).
分组,得到成绩分布的频率分布直方图(如图).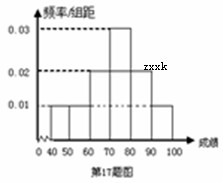
(Ⅰ)若规定60分以上(包括60分)为合格,计算高一年级这次知识竞赛的合格率;
(Ⅱ)统计方法中,同一组数据常用该组区间的中点值作为代表,据此,估计高一年级这次知识竞赛的学生的平均成绩;
(Ⅲ)若高二年级这次知识竞赛的合格率为60%,由以上统计数据填写下面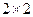 列联表,并问是否有99%的把握认为“这次知识竞赛的成绩与年级有关系”。
列联表,并问是否有99%的把握认为“这次知识竞赛的成绩与年级有关系”。
| |
高一 |
高二 |
合计 |
| 合格人数 |
|
|
|
| 不合格人数 |
|
|
|
| 合计 |
|
|
|
参考数据与公式:
由列联表中数据计算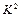 的公式
的公式 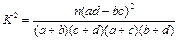
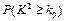 |
0.10 |
0.05 |
0.010 |
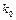 |
2.706 |
3.841 |
6.635 |
临界值表
(本小题满分14分)
已知m>0,设命题 函数
函数 在
在 上单调递减;命题
上单调递减;命题 关于x的不等式
关于x的不等式 的解集为R。若命题
的解集为R。若命题 与
与 有且仅有一个正确,求
有且仅有一个正确,求 的取值范围。
的取值范围。
在平面直角坐标系xOy中,点A(-1,-2)、B(2,3)、C(-2,-1)。
(1)求以线段AB、AC为邻边的平行四边形两条对角线的长;
(2)设实数t满足 (
(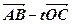 )·
)· =0,求t的值
=0,求t的值
.(本小题满分14分)
已知函数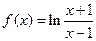
(Ⅰ)求函数的定 义域,并证明
义域,并证明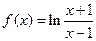 在定义域上是奇函数;
在定义域上是奇函数;
(Ⅱ)若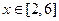
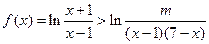 恒成立,求实数
恒成立,求实数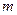 的取值范围;
的取值范围;
(Ⅲ)当 时,试比较
时,试比较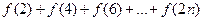 与
与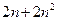 的大小关系
的大小关系
(本小题满分14分 )
)
已知等差数列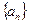 的公差为
的公差为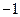 , 且
, 且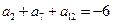 ,
,
(1)求数列 的通项公式
的通项公式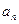 与前
与前 项和
项和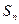 ;
;
(2)将数列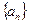 的前
的前 项抽去其中一项后,剩下三项按原来顺序恰为等比数列
项抽去其中一项后,剩下三项按原来顺序恰为等比数列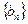
的前3项,记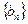 的前
的前 项和为
项和为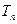 , 若存在
, 若存在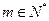 , 使对任意
, 使对任意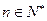 总有
总有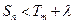 恒成立, 求实数
恒成立, 求实数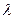 的取值范围.K
的取值范围.K
((本小题满分14分)
已知圆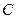 的圆心为
的圆心为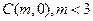 ,半径为
,半径为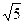 ,圆
,圆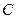 与椭圆
与椭圆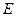 :
: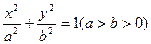 有一个公共点
有一个公共点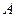 (3,1),
(3,1),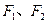 分别是椭圆的左、右焦点.
分别是椭圆的左、右焦点.
(1)求圆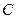 的标准方程;
的标准方程;
(2)若点P的坐标为(4,4),试探究斜率为k的直线
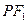 与圆
与圆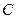 能否相切,若能,求出椭圆
能否相切,若能,求出椭圆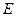 和直线
和直线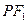 的方程;若不能,请说明理由.
的方程;若不能,请说明理由.