某电视生产企业有A、B两种型号的电视机参加家电下乡活动,若企业投放A、B两种型号电视机的价值分别为a、b万元,则农民购买电视机获得的补贴分别为 万元(m>0且为常数).已知该企业投放总价值为10万元的A、B两种型号的电视机,且A、B两种型号的投放金额都不低于1万元.
万元(m>0且为常数).已知该企业投放总价值为10万元的A、B两种型号的电视机,且A、B两种型号的投放金额都不低于1万元.
(1)请你选择自变量,将这次活动中农民得到的总补贴表示为它的函数,并求其定义域;
(2)求当投放B型电视机的金额为多少万元时,农民得到的总补贴最大?
(本小题满分12分)
若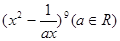 的展开式中
的展开式中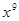 的系数是
的系数是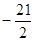 .
.
(1)求展开式中的常数项;
(2)求 的值.
的值.
已知等差数列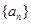 的前
的前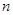 项和为
项和为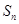 ,且
,且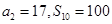 .
.
(I)求数列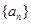 的通项公式;
的通项公式;
(II)若数列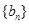 满足
满足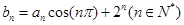 ,求数列
,求数列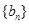 的前
的前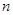 项和.
项和.
某小区要建一座八边形的休闲小区,如右图它在主体造型的平面图是由两个相同的矩形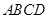 和
和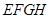 构成的面积为200平方米的十字形地域。计划在正方形
构成的面积为200平方米的十字形地域。计划在正方形 上建一座花坛,造价每平方米4200元,并在四周的四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为每平方米210元,再在四个空角上铺草坪,造价为每平方米80元。
上建一座花坛,造价每平方米4200元,并在四周的四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为每平方米210元,再在四个空角上铺草坪,造价为每平方米80元。
⑴设总造价为 元,
元, 长为
长为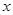 米,试求
米,试求 关于
关于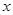 的函数关系式;
的函数关系式;
⑵当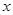 为何值,
为何值, 取得最小值?并求出这个最小值.
取得最小值?并求出这个最小值.
如图,已知点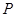 在圆柱
在圆柱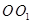 的底面圆
的底面圆 上,
上,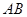 为圆
为圆 的直径,圆柱
的直径,圆柱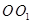 的表面积为
的表面积为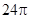 ,
, ,
, 。
。
(1)求三棱锥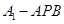 的体积。
的体积。
(2)求异面直线 与
与 所成角的余弦值;
所成角的余弦值;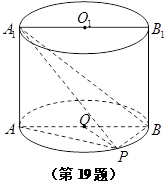
 中内角
中内角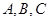 的对边分别为
的对边分别为 ,向量
,向量 且
且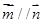 (1)求锐角
(1)求锐角 的大小;(2)如果
的大小;(2)如果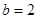 ,求
,求 的面积
的面积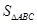 的最大值
的最大值