请认真阅读下列材料：
“杨辉三角” (1261年)是中国古代重要的数学成就,它比西方的“帕斯卡三角”(1653年)早了300多年(如表1).在“杨辉三角”的基础上德国数学家莱布尼兹发现了
下面的单位分数三角形（单位分数是分子为1,分母为正整数的分数）,称为莱布尼兹三角形(如表2)
请回答下列问题:
（I）记
为表1中第n行各个数字之和,求
，并归纳出；
（II）根据表2前5行的规律依次写出第6行的数.
将A、B两枚均匀的骰子各
抛掷一次，向上的点数分别为
，
，
（I）共有多少种结果？
（II）“
”的概率是多少？
（本小题满分14分）设函数
（1）求
的单调区间和极值；
（2）若关于
的方程
有
个不同实根，求实数
的取值范围；
（3）已知当
时，
恒成立，求实数
的取值范围。
（本小题满分14分）在
中，角
的对边分别为
，已知
，
，
．
（1）求
的值；
（2）求
的值；
（3）求的面积。
（本小题满分13分）已知函数
，其中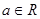
（1）当
时，求曲线
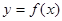在点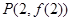
处的切线方程;
（2）若函数
在区间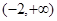
为增函数，求
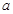的取值范围。
在圆柱
的底面圆
上，
为圆
，
，
。
的体积。
与
所成角的余弦值；