本题(1)、(2)、(3)三个选答题,每小题7分,请考生任选2题作答,满分14分,如果多做,则按所做的前两题计分.作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中。
(1)(本小题满分7分)选修4-2:矩阵与变换
已知向量 =
= ,变换T的矩阵为A=
,变换T的矩阵为A= ,平面上的点P(1,1)在变换T
,平面上的点P(1,1)在变换T
作用下得到点P′(3,3),求A4 .
.
(2)(本小题满分7分)选修4-4:坐标系与参数方程
直线 与圆
与圆 (
( >0)相交于A、B两点,设
>0)相交于A、B两点,设
P(-1,0),且|PA|:|PB|=1:2,求实数 的值
的值
(3)(本小题满分7分)选修4-5:不等式选讲
对于x∈R,不等式|x-1|+|x-2|≥ 2+
2+ 2恒成立,试求2
2恒成立,试求2 +
+ 的最大值。
的最大值。
将边长为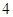 的正方形
的正方形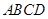 和等腰直角三角形
和等腰直角三角形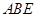 按图拼为新的几何图形,
按图拼为新的几何图形,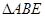 中,
中, ,连结
,连结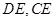 ,若
,若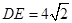 ,
, 为
为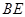 中点
中点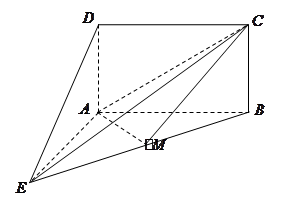
(Ⅰ)求 与
与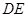 所成角的大小;
所成角的大小;
(Ⅱ)若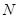 为
为 中点,证明:
中点,证明: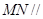 平面
平面 ;
;
(Ⅲ)证明:平面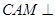 平面
平面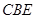
某旅游推介活动晚会进行嘉宾现场抽奖活动,抽奖规则是:抽奖盒中装有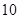 个大小相同的小球,分别印有“多彩十艺节”和“美丽泉城行”两种标志,摇匀后,参加者每次从盒中同时抽取两个小球,若抽到两个球都印有“多彩十艺节”标志即可获奖.
个大小相同的小球,分别印有“多彩十艺节”和“美丽泉城行”两种标志,摇匀后,参加者每次从盒中同时抽取两个小球,若抽到两个球都印有“多彩十艺节”标志即可获奖.
(I)活动开始后,一位参加者问:盒中有几个“多彩十艺节”球?主持人笑说:我只知道从盒中同时抽两球不都是“美丽泉城行”标志的概率是 ,求抽奖者获奖的概率;
,求抽奖者获奖的概率;
(Ⅱ)上面条件下,现有甲、乙、丙、丁四人依次抽奖,抽后放回,另一个人再抽,用 表示获奖的人数,求
表示获奖的人数,求 的分布列及
的分布列及 .
.
已知函数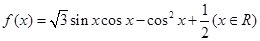 .
.
(1)求函数 的最小正周期;
的最小正周期;
(2)求函数 在区间
在区间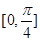 上的函数值的取值范围.
上的函数值的取值范围.
已知函数 .
.
(1)若不等式 的解集为
的解集为 ,求实数
,求实数 的值;
的值;
(2)在(Ⅰ)的条件下,若存在实数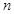 使
使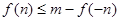 成立,求实数
成立,求实数 的取值范围.
的取值范围.
已知极坐标的极点在平面直角坐标系的原点 处,极轴与
处,极轴与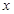 轴的正半轴重合,且长度单位相同.直线
轴的正半轴重合,且长度单位相同.直线 的极坐标方程为:
的极坐标方程为: ,点
,点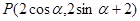 ,参数
,参数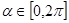 .
.
(Ⅰ)求点 轨迹的直角坐标方程;(Ⅱ)求点
轨迹的直角坐标方程;(Ⅱ)求点 到直线
到直线 距离的最大值.
距离的最大值.