(13分)已知椭圆C的中心在坐标原点,离心率 ,且其中一个焦点与抛物线
,且其中一个焦点与抛物线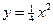 的焦点重合.
的焦点重合.
(1)求椭圆C的方程;
(2)过点S(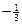 ,0)的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过点T,若存在,求出点T的坐标;若不存在,请说明理由.
,0)的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过点T,若存在,求出点T的坐标;若不存在,请说明理由.
选修4—5:不等式选讲
设函数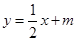 .
.
(1)当 时,求函数
时,求函数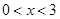 的定义域;
的定义域;
(2)若函数 的定义域为R,试求
的定义域为R,试求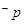 的取值范围.
的取值范围.
选修4—4:坐标系与参数方程
在平面直角坐标系xOy中,以O为极点,Ox为极轴建立极坐标系,且两种坐标系长度单位一致. 已知直线l的极坐标方程为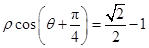 ,圆C在直角坐标系中的参数方程为
,圆C在直角坐标系中的参数方程为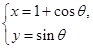 (
(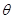 为参数),求直线l与圆C的公共点的个数.
为参数),求直线l与圆C的公共点的个数.
(本小题满分14分)如图,在正三棱柱ABC-A1B1C1中,D、E分别为CC1、A1B1的中点.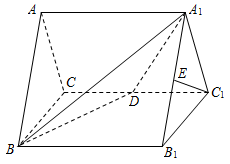
求证:C1E∥平面A1BD;
(2)求证:平面ABB1A1⊥平面A1BD.
(本小题满分14分) 在△ABC中,a,b,c分别为内角A,B,C的对边,且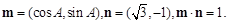
(1)求A的大小;
(2)现给出三个条件:①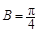 ;②a=2;③
;②a=2;③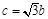 .请从中选择两个条件,使得确定的△ABC的面积最大.
.请从中选择两个条件,使得确定的△ABC的面积最大.
已知函数f(x)=x2-4,设曲线y=f(x)在点(xn,f(xn))处的切线与x轴的交点为(xn+1,0)(n∈N +),其中xn为正实数.
(1)用xn表示xn+1;
(2)若x1=4,记an=lg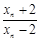 ,证明数列{an}成等比数列,并求数列{xn}的通项公式;
,证明数列{an}成等比数列,并求数列{xn}的通项公式;
(3)若x1=4,bn=xn-2,Tn是数列{bn}的前n项和,证明Tn<3.