(14分)已知椭圆C的中心在坐标原点,焦点在x轴上,离心率 .直线
.直线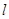 :
: 与椭圆C相交于
与椭圆C相交于 两点, 且
两点, 且 .
.
(1)求椭圆C的方程;
(2)点P(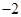 ,0),A、B为椭圆C上的动点,当
,0),A、B为椭圆C上的动点,当 时,求证:直线AB恒过一个定点.并求出该定点的坐标.
时,求证:直线AB恒过一个定点.并求出该定点的坐标.

已知函数f(x)=(x+a)(bx+2a)是偶函数 (其中a,b是常数),且它的值域为  ,
,
(Ⅰ)求f(x)的解析式
将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,将得到的点数分别记为 .
.
(Ⅰ)求直线 与圆
与圆 有公共点的概率;
有公共点的概率;
(Ⅱ)求方程组 只有正数解的概率。
只有正数解的概率。
已知函数f(x)=Asin(x+φ)(A>0,0<φ<π),x∈R的最大值是1,其图象经过点
(Ⅰ)求f(x)的解析式;
(Ⅱ)
2011年3月5日某校组织同学听取了温家宝总理所作的政府工作报告,并进行了检测,从参加检测的高一学生中随机抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)求分数在[70,80)内的频率,并补全这个频率分布直方图;
(Ⅱ)请根据频率分布直方图估计本次考试中的成绩的平均分及中位数(可保留一位小数).