(本小题14分)
锐角 中,内角
中,内角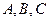 所对边
所对边 ,
,
向量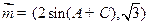 ,
,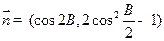 ,且向量
,且向量 共线,
共线,
(1)求角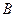 (2)若边
(2)若边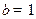 ,求
,求 的面积的最大值
的面积的最大值
当室内的有毒细菌开始增加时,就要使用杀菌剂.刚开始使用的时候,细菌数量还会继续增加,随着时间的增加,它增加幅度逐渐变小,到一定时间,细菌数量开始减少.如果使用杀菌剂t小时后的细菌数量为b(t)=105+104t-103t2.
(1)求细菌在t=5与t=10时的瞬时速度;(2)细菌在哪段时间增加,在哪段时间减少?为什么?
已知某工厂生产 件产品的成本为
件产品的成本为 (元),问:(1)要使平均成本最低,应生产多少件产品?(2)若产品以每件500元售出,要使利润最大,应生产多少件产品?
(元),问:(1)要使平均成本最低,应生产多少件产品?(2)若产品以每件500元售出,要使利润最大,应生产多少件产品?
已知函数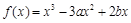 在
在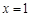 处有极小值
处有极小值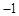 ,试求
,试求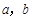 的值,并求出
的值,并求出 的单调区间.
的单调区间.
已知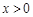 ,证明不等式
,证明不等式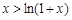 .
.
在某海滨城市附近海面有一台风,据检测,当前台风中心位于城市O(如图)的东偏南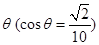 方向300 km的海面P处,并以20 km / h的速度向西偏北
方向300 km的海面P处,并以20 km / h的速度向西偏北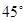 的方向移动,台风侵袭的范围为圆形区域,当前半径为60 km ,并以10 km / h的速度不断增加,问几小时后该城市开始受到台风的侵袭?持续多长时间?
的方向移动,台风侵袭的范围为圆形区域,当前半径为60 km ,并以10 km / h的速度不断增加,问几小时后该城市开始受到台风的侵袭?持续多长时间?