已知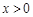 ,证明不等式
,证明不等式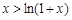 .
.
已知
的角
所对的边分别是
,设向量
.
(1)若
,求证:
为等腰三角形;
(2)若
,边长
,角
,求
的面积.
已知
是公差为
的等差数列,
是公比为
的等比数列.
(1)若
,是否存在
,有
说明理由;
(2)找出所有数列
和
,使对一切
,
,并说明理由;
(3)若
试确定所有的
,使数列
中存在某个连续
项的和是数列
中的一项,请证明.
已知函数
的反函数.定义:若对给定的实数
,函数
与
互为反函数,则称
满足"
和性质";若函数
与
互为反函数,则称
满足"
积性质".
(1)判断函数
是否满足"1和性质",并说明理由;
(2)求所有满足"2和性质"的一次函数;
(3)设函数
对任何
,满足"
积性质".求
的表达式.
已知双曲线 ,设过点 的直线 的方向向量
(1)当直线
与双曲线
的一条渐近线
平行时,求直线
的方程及
与
的距离;
(2)证明:当
时,在双曲线
的右支上不存在点
,使之到直线
的距离为
.
有时可用函数
描述学习某学科知识的掌握程度,其中
表示某学科知识的学习次数(
),
表示对该学科知识的掌握程度,正实数
与学科知识有关.
(1)证明:当
时,掌握程度的增加量
总是下降;
(2)根据经验,学科甲、乙、丙对应的a的取值区间分别为
,
,
.当学习某学科知识6次时,掌握程度是85%,请确定相应的学科.