如图所示,半径R = 0.8m的四分之一光滑圆弧轨道位于竖直平面内,与长CD = 2.0m的绝缘水平面平滑连接。水平面右侧空间存在互相垂直的匀强电场和匀强磁场,电场强度E = 40N/C,方向竖直向上,磁场的磁感应强度B = 1.0T,方向垂直纸面向外。两个质量均为m = 2.0×10-6kg的小球a和b,a球不带电,b球带q = 1.0×10-6C的正电,并静止于水平面右边缘处。将a球从圆弧轨道顶端由静止释放,运动到D点与b球发生正碰,碰撞时间极短,碰后两球粘合在一起飞入复合场中,最后落在地面上的P点。已知小球a在水平面上运动时所受的摩擦阻力 f = 0.1mg, PN =
f = 0.1mg, PN = ,取g =10m/s2。a、b均可作为质点。(结果保留三位有效数字)求:
,取g =10m/s2。a、b均可作为质点。(结果保留三位有效数字)求:
(1)小球a与b相碰后瞬间速度的大小v
(2)水平面离地面的高度h
(3)从小球a开始释放到落地前瞬间的整个运动过程中,ab系统损失的机械能ΔE。
某校课外活动小组,自制一枚“火箭”,火箭在地面时的质量为3kg。设火箭发射实验时,始终在垂直于地面的方向上运动。火箭点火后可认为作匀加速运动,经过4s到达离地面40m高处燃料恰好用完。若空气阻力忽略不计,g取10m/s2。求:
(1)燃料恰好用完时火箭的速度为多大?
(2)火箭上升离地面的最大高度是多大?
如图所示,在长为2L、宽为L的ABCD区域内有一半的空间存在场强为E、方向平行于BC边的匀强电场,现有一个质量为m,电量为e的电子,以平行于AB边的速度v0从区域的左上角A点射入该区域,不计电子所受的重力,则: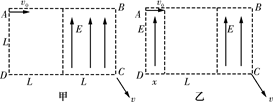
(1)当无电场的区域位于左侧时(如图甲),求电子射出ABCD区域时的动能;
(2)当无电场区域的左边界距AD的距离为x时(如图乙),要使这个电子能从区域的右下角的C点射出,电子的初速度v0应满足什么条件。
磕头虫是一种不用足跳但又善于跳高的小甲虫。当它腹朝天、背朝地躺在地面上时,将头用力向后仰,拱起体背,在身下形成一个三角形空区,然后猛然收缩体内背纵肌,使重心迅速向下加速,背部猛烈撞击地面,地面反作用力便将其弹向空中。弹射录像显示,磕头虫拱背后重心向下加速(视为匀加速)的距离大约为h1=0.8mm,弹射最大高度为h2=24cm。而人原地起跳方式是,先屈腿下蹲,然后突然蹬地向上加速,假想人的加速度与磕头虫加速过程的加速度大小相等,如果加速过程(视为匀加速)重心上升高度为H1=0.4m,求人离地后重心上升的最大高度H2。(空气阻力不计,设磕头虫撞击地面和弹起的速率相等)
如图所示,水平放置的平行板电容器与电压恒定的直流电源相连,两极板间距离d=10cm。电容器的电容C=2pF。距下极板4cm处有一质量m=0.01kg的不带电小球由静止落下。小球和下极板碰撞后带上了q=1.0×10-8C的电荷,反跳的高度为8cm,如果小球和下板碰撞时没有机械能损失,试求该电容器的带电量。(取g=10m/s2)
如图所示,在足够长的光滑绝缘水平直线轨道上方h高度的P点,固定电荷量为+Q的点电荷。一质量为m、电荷量为-q的物块(可视为质点),从轨道上的A点以初速度v0沿轨道向右运动,且始终不离开轨道。已知点电荷产生的电场在A、B两点的电势分别为φ1、φ2,PA连线与水平轨道的夹角为60°。试求:
(1)物块在A点时的加速度大小;
(2)物块在运动过程中的最大速度。