21.(19分)
图为“双聚焦分析器”质谱仪的结构示意图,其中,加速电场的电压为U,静电分析器中与圆心01等距离的各点场强大小相等、方向沿径向,磁分析器中以02为圆心、圆心角为90o的扇形区域内,分布着方向垂直于纸面的匀强磁场,其左边界与静电分析器的右端面平行。由离子源发出的一质量为m、电荷量为g的正离子(初速度为零,重力不计)经加速电场加速后,从M点垂直于电场方向进入静电分析器,沿半径为R的四分之一圆弧轨迹做匀速圆周运动,从N点射出,接着由P点垂直磁分析器的左边界射入,最后垂直于下边界从Q点射出并进入收集器。已知Q点与圆心02的距离为d。求:
(1)磁分析器中磁场的磁感应强度B的大小和方向;
(2)静电分析器中离子运动轨迹处电场强度E的大小;
(3)现将离子换成质量为0.9m、电荷量仍为g的另一种正离子,其它条件不变。试直接指出该离子进入磁分析器时的位置,它射出磁场的位置在Q点的左侧还是右侧?
小明是学校的升旗手,他每次升旗都做到了在庄严的《义勇军进行曲》响起时开始升旗,当国歌结束时恰好五星红旗升到了高高的旗杆顶端。已知国歌从响起到结束的时间是48 s,旗杆高度是19 m,红旗从离地面1.4 m处开始升起。若设小明升旗时先拉动绳子使红旗向上匀加速运动,时间持续4 s,然后使红旗做匀速运动,最后使红旗做匀减速运动,加速度大小与开始升起时的加速度大小相同,红旗到达旗杆顶端时的速度恰好为零。试计算
(1)红旗匀速运动的速度大小;
(2)小明升旗时使红旗向上做匀加速运动的加速度大小。
一辆卡车初速度为v0=10m/s,以a=2m/s2的加速度行驶,求:
(1)卡车在3s末的速度v
(2)卡车在6s内的位移x6与平均速度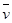
(3)卡车在第6s内的位移x
如图所示,物体A放在足够长的木板B上,木板B静止于水平面。t=0时,电动机通过水平细绳以恒力F拉木板B,使它做初速度为零,加速度aB=1.0m/s2的匀加速直线运动。已知A的质量mA和B的质量mB均为2.0kg,A、B之间的动摩擦因数μ1=0.05,B与水平面之间的动摩擦因数μ2=0.1,最大静摩擦力与滑动摩擦力大小视为相等,重力加速度g取10m/s2。求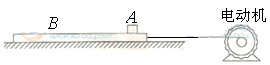
(1)物体A刚运动时的加速度aA
(2)t1=1.0s时,电动机的输出功率P;
(3)若t1=1.0s时,将电动机的输出功率立即调整为P1=5W,并在以后的运动过程中始终保持这一功率不变,t2=3.8s时物体A的速度为1.2m/s。则在t1=1.0s到t2=3.8s这段时间内木板B的位移为多少?
如图所示,A、B质量分别为mA=1kg,mB=2kg,AB间用弹簧连接着,弹簧弹性系数k=100N/m,轻绳一端系在A上,另一端跨过定滑轮,B为套在轻绳上的光滑圆环,另一圆环C固定在桌边,B被C挡住而静止在C上,若开始时作用在绳子另一端的拉力F为零,此时A处于静止且刚没接触地面。现用恒定拉力F=15N拉绳子,恰能使B离开C但不能继续上升,不计摩擦且弹簧没超过弹性限度,求
(1)B刚要离开C时A的加速度, (2)若把拉力F改为F=30N,则B刚要离开C时,A的速度。
如图所示,AC为光滑竖直杆,ABC为构成直角的光滑L形轨道,B处有一小圆弧连接可使小球顺利转弯,并且A、B、C三点正好是圆上三点,而AC正好是该圆的直径,如果套在杆上的小球
自A点静止释放(图中小球未画出),分别沿ABC曲轨道和AC直轨道运动到C点,如果沿ABC曲轨道运动的时间是沿AC直轨道运动所用时间的1.5倍,求AC与AB夹角α的值