如图,四棱锥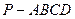 中,底面
中,底面 是边长为2的正方形,
是边长为2的正方形, ,
,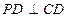 ,
,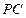 与底面
与底面 所成的角的正切值为
所成的角的正切值为 ,
,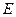 为
为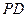 中点.
中点.
(1) 求二面角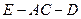 的大小.
的大小.
(2) 在线段 上是否存在点
上是否存在点 ,使得点
,使得点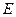 到平面
到平面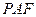 的距离为
的距离为 .若存在,确定点
.若存在,确定点 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
计算下列各式的值:
(1) ;(2)
;(2) .
.
已知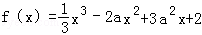 的定义域是[0,4].
的定义域是[0,4].
(1)若f(x)的极值点是x=3,求a的值;
(2)若f(x)是单峰函数,求a的取值范围.
设f(x)是定义在[0,1]上的函数,若存在x*∈(0,1),使得f(x)在[0,x•]上单调递增,在[x•,1]单调递减,则称f(x)为[0,1]上的单峰函数,x•为峰点,包含峰点的区间为含峰区间.
对任意的[0,1]上的单峰函数f(x),下面研究缩短其含峰区间长度的方法.
(Ⅰ)证明:对任意的x1,x2∈(0,1),x1<x2,若f(x1)≥f(x2),则(0,x2)为含峰区间;若f(x1)≤f(x2),则(x1,1)为含峰区间;
(Ⅱ)对给定的r(0<r<0.5),证明:存在x1,x2∈(0,1),满足x2﹣x1≥2r,使得由(Ⅰ)确定的含峰区间的长度不大于0.5+r;
(Ⅲ)选取x1,x2∈(0,1),x1<x2由(Ⅰ)可确定含峰区间为(0,x2)或(x1,1),在所得的含峰区间内选取x3,由x3与x1或x3与x2类似地可确定是一个新的含峰区间.在第一次确定的含峰区间为(0,x2)的情况下,试确定x1,x2,x3的值,满足两两之差的绝对值不小于0.02且使得新的含峰区间的长度缩短到0.34.
(区间长度等于区间的右端点与左端点之差).
分解因式
(1)a4﹣6a2﹣27;
(2)a4+4b2c2﹣a2b2﹣4a2c2.
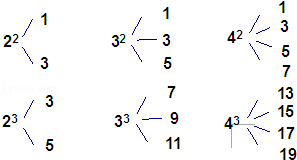
如图,对于大于1的自然数m的n次幂可用奇数进行如图所示的“分裂”,仿此,记53的“分裂”中的最小数为a,而52的“分裂”中最大的数是b,则a+b=.