如图5,四边形 是圆柱
是圆柱 的轴截面,点
的轴截面,点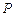 在圆柱
在圆柱 的底面圆周上,
的底面圆周上,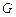 是
是 的中点,圆柱
的中点,圆柱 的底面圆的半径
的底面圆的半径 ,侧面积为
,侧面积为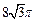 ,
,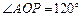 .
.
(1)求证: ;
;
(2)求二面角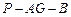 的平面角的余弦值.
的平面角的余弦值. 
如图,在长方体 中, 分别是棱 上的点, .
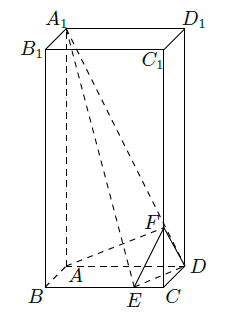
(1)求异面直线
与
所成角的余弦值;
(2)证明
平面
;
(3)求二面角 的正弦值.
某射手每次射击击中目标的概率是
,且各次射击的结果互不影响。
(Ⅰ)假设这名射手射击5次,求恰有2次击中目标的概率
(Ⅱ)假设这名射手射击5次,求有3次连续击中目标。另外2次未击中目标的概率;
(Ⅲ)假设这名射手射击3次,每次射击,击中目标得1分,未击中目标得0分,在3次射击中,若有2次连续击中,而另外1次未击中,则额外加1分;若3次全击中,则额外加3分,记
为射手射击3次后的总的分数,求
的分布列。
已知函数
(Ⅰ)求函数
的最小正周期及在区间
上的最大值和最小值;
(Ⅱ)若
,求
的值。
设函数
(Ⅰ)画出函数
的图像
(Ⅱ)若不等式
的解集非空,求
的取值范围.
已知直线
(
为参数),
(
为参数),
(Ⅰ)当
时,求
与
的交点坐标;
(Ⅱ)过坐标原点
做
的垂线,垂足为
,
为
中点,当
变化时,求
点的轨迹的参数方程,并指出它是什么曲线.